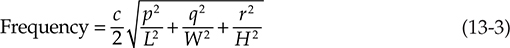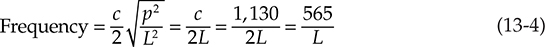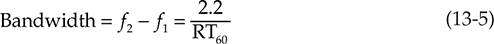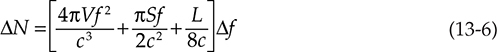《声学手册(第七版)》第十三章

第 13 章

模态共振

封闭空间中的声音行为与自由场中的声音有根本的不同。在自由场中，声音离开源并向外传播，没有受到阻碍。例如，很容易确定离源的任何距离处的声压级。在大多数封闭空间中，来自源的声音会从边界表面（如墙壁、地板和天花板）反射。在封闭空间中的任何点处的结果声压级是直接声音和反射声音的组合。特别是，模态共振被建立；在封闭空间的不同位置，声压级将不同，并且还会根据频率而变化。这些共振频率及其引起的变化是封闭空间尺寸的函数。

大多数房间可以被视为封闭空间；它们本质上是空气容器。因此，它们表现出模态共振，即能量集中的首选频率。同样，这些共振会产生能量减少的频率。这种复杂的能量分布存在于整个房间的三维空间中。许多乐器在其构造中使用管道或管道；这些也作为封闭空间运作，并表现出模态共振。改变模态共振的参数会改变音乐音调。

我们生活的大多数时间都在封闭空间中；因此，我们的声学生活受到这些大型共振器影响。无论如何，房间共振会影响我们在室内时听到的声音。

早期实验和示例

赫尔曼·冯·黑尔姆霍兹进行了一系列关于共振器的早期声学实验。他的共振器是一系列大小不同的金属球，每个球都配有一个颈部，看起来有点像化学实验室中的圆底烧瓶。除了颈部外，还有另一个小开口，他将其放在耳朵附近。不同大小的共振器在不同频率上共振，通过将共振器的颈部对准研究中的声音，他可以利用不同共振器的音量来估计每个频率上的能量。

在赫尔曼·冯·黑尔姆霍兹之前的很长一段时间，这个原理就已经有了许多应用。一千年前，瑞典和丹麦的教堂墙壁中嵌入了共振器，其口与墙面齐平，显然是为了吸收声音。一些现代建筑的内墙使用带有狭缝的混凝土块，导致内部形成封闭的共振腔。从房间中吸收的声音引起共振器以特定频率振动。部分能量被吸收，部分被重新辐射。重新辐射的能量朝各个方向发射，有助于房间中声音的扩散。共振器的原理，尽管古老，不断出现在新的应用中。

管道中的共振

封闭管道的两端，如图13-1A所示，可类比为房间的两面相对的墙壁。该管道为我们提供了一个简单的一维示例；在矩形房间相对的两面墙之间发生的情况可以在不受其他四个表面反射干扰的情况下进行研究。该管道是一个共振器，当以某种方式激发时，能够以其特定频率振动。我们将考虑在声波波长远大于管道直径的情况下，使声音能够沿着管道传播。当在风琴管的边缘吹过嘴唇时，管道内的气柱将开始振动。更精确地说，对于我们的实验，可以在两端都封闭的管道内放置一个小型扬声器。正弦波信号被送入扬声器并在频率上变化。在与扬声器辐射的频率与管道的固有频率相符的时候，我们能够从与扬声器相对的管道末端的小听孔中听到扬声器辐射的音调。随着频率的增加，直到频率达到f₁时，没有发现异常。在这个频率f₁，来自扬声器的适度能量被强烈增强，听到相对较大的声音。我们注意到这个频率的波长是管道长度的两倍。随着频率的增加，直到达到2f₁的频率，声音的响度再次较低，此时又注意到另一个强烈的增强。这样的共振峰也可以在3f₁、4f₁...以及所有f₁的倍数处检测到。

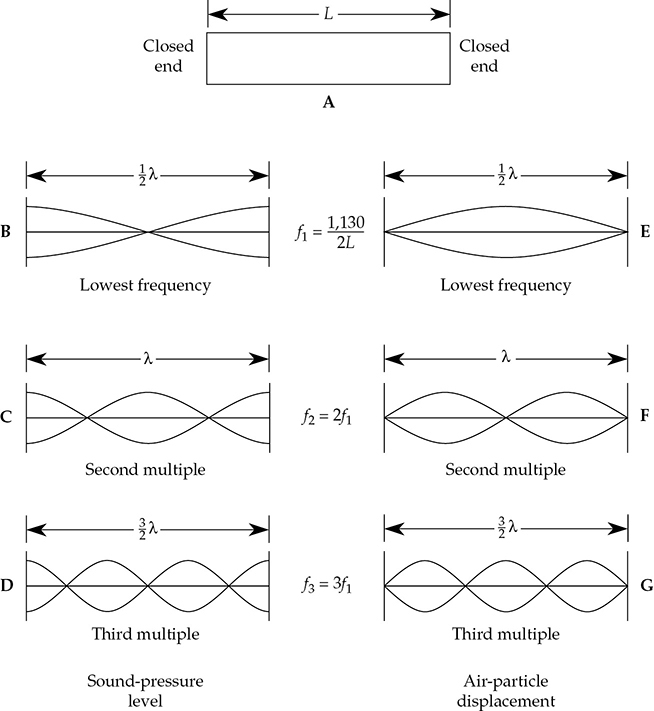
图13-1 两端封闭的管道演示了在房间的两个相对墙之间发生共振的过程。管道的长度（在房间中墙之间的距离）确定了共振的特征频率及其谐波。（A）封闭管道。（B）f₁的声压级图。 （C）f₂的声压级图。 （D）f₃的声压级图。 （E）f₁的空气颗粒位移图。 （F）f₂的空气颗粒位移图。 （G）f₃的空气颗粒位移图。

现在让我们假设我们可以测量和记录沿管道长度的声压。图13-1B、C和D显示了在三种不同的激励频率下沿管道的声压变化。右行的声波从右端反射回来，以与自身极性相反的声波形式返回（由半周期延迟），然后向左行进。向左行进的波与向右行进的波通过叠加创造出纵向固定频率的立体声波，以及该频率的倍数。这些立体波在反射表面之间具有消除（节点）和增强（反节点）的区域。我们注意到封闭管道的共振频率f_n由管道的长度确定。特别地，

其中 n = 整数 ≥ 1

      L = 管道长度，英尺或米

      c = 声速 = 1,130 英尺/秒或344 米/秒

例如，如果封闭管道的长度为5英尺，则基本共振频率 f₁ 为 1,130/10 = 113 Hz。第二共振频率 f₂ 为 (2)(1,130)/10 = 226 Hz，以此类推。

在发出f₁频率的时候，如图13-1B所示，通过沿着管道插入微小孔的测量探头可以检测到管道中心处的零压力，靠近管道封闭端的高压力等等。在2f₁和3f₁处也可以观察到类似的节点（最小值）和反节点（最大值），如图13-1C和D所示。同样，其他共振频率会存在于f₁的高阶倍数处。

同样，房间的尺寸以某种方式决定了其特征频率，就好像有一个南北管道、一个东西管道和一个垂直管道，这些管道分别对应于房间的长度、宽度和高度。换句话说，房间的行为与封闭管道相同，但是在三维空间中。此外，房间还可以展示从两个以上表面反射的其他类型的模式。

我们还注意到在任何立体波中，空气颗粒的位移是精确定义的，如图13-1E、F和G所示。特别是，在任何点上，粒子位移与声压级完全反相；在每个压力反节点处有一个位移节点，而在每个压力节点处有一个位移反节点。例如，在封闭管道的两端，粒子位移始终为零。对于最低模式（见图13-1E），粒子位移在中心点最大；对于任何模式，尽管物理距离不同，但最大粒子位移的第一个位置（和最小粒子速度）对应于λ/4。这解释了为什么在封闭管道和房间中，多孔吸声材料在距离边界λ/4处最有效。

任何有反射墙壁的房间都会呈现共振效应及由房间尺寸相关的特定频率的声音增强效果。在远离这些特征频率的频率下激励空气会导致声音变得更弱。

想象一下自己在图13-1D所示的管道内。在那个共振频率下，你会听到声压随着你穿过管道的长度而升高和降低。一个在房间内的人，在某种程度上，就像是在两端封闭的大管道内。然而，有一个重要的区别；现在是一个三维而不是基本上是一维的系统，就像这个管道一样。当房间的墙壁具有反射性时，与房间的长度相关联的有一个特征的共振频率，与宽度相关联的有另一个，高度相关联的仍有一个。在正方形房间的情况下，所有三个共振频率重合，以在基本特征共振频率和其倍数处提供强大的增强。这导致房间内的响应非常不均匀，因此，应该避免使用正方形房间或任何具有相等尺寸的房间。

室内反射

任何人都能体会到室内和室外声音条件之间的差异。在室外的开放空间中，唯一的反射平面可能是地面。如果地面上覆盖着一英尺厚的吸声效果良好的雪，与20英尺远处的人进行对话可能会比较困难。而在室内，声能被封闭，使得相同的努力能产生更大的声音。在礼堂里，演讲者可以被数百人听到和理解，而无需除了反射表面之外的任何增强。

考虑从单个墙壁反射的声音。在图13-2中，声源S离刚性墙壁有一定距离。球形波前（实线，向右传播）从这个表面反射出去（虚线）。从表面向左传播的反射作用上，就好像它们是从另一个相同的点源，即图像源I，发射出来的一样，图像源距离反射表面相等，但在相对的另一侧。这是一个在自由空间中具有一个源、一个图像和一个反射表面的最简单情况。

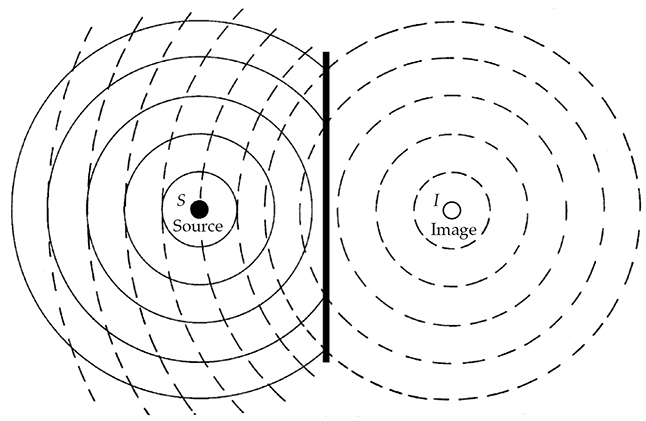
图13-2 由点源S辐射的声音被刚性墙壁反射。反射波可以看作是来自I，即S的图像。

现在让我们将图13-2中孤立的反射表面视为矩形房间的东墙，如图13-3所示。源S仍然在房间的东墙上有它的图像，现在标记为I_E。源还有其他的图像。I_N是在北墙反射表面上的S的图像，I_W是在西墙上的S的图像，I_S是在南墙上的S的图像。想象一下I_F，地板上的图像，以及I_C，天花板上的图像。所有这六个图像，就像S一样，都在将声能送回房间。由于在反射表面上的吸收，它们在房间的给定点P的贡献会稍微减弱，但它们都起到了一定的作用。

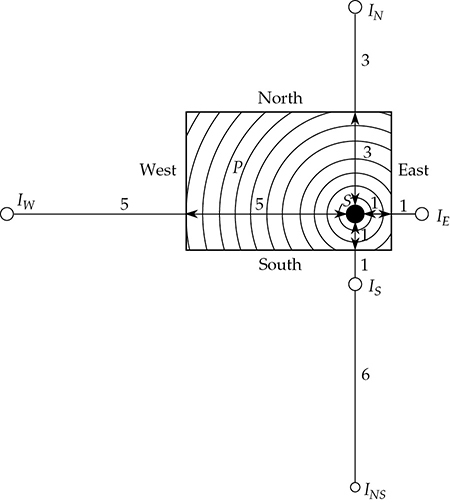
图13-3 在一个封闭空间中，源S有六个主要图像，分别位于封闭空间的六个表面上。由多次反射和来自多个表面的反射产生了无限多个其他图像。点P处的声强由S的直接声音加上所有图像的贡献的矢量和组成。

还有从反射多个表面的声音产生的图像。例如，I_NS图像是由离开S，从北墙反射，然后从南墙反射产生的。同样，其他表面产生相同的多次反射。而且，这个过程会继续，例如从北到南再到北的反射，无穷无尽。最后，其他声音可能以许多其他角度反射，例如从北、西、南和东的每堵墙壁反射。

经过许多表面反射后，图像变得非常微弱，可以忽略不计以简化问题。无论如何，在房间中点P处的声音场包括来自源S的直接声音以及来自S的所有图像的单一或多次反射的矢量和。

两面共振

图13-4 展示了两个平行的、无限延伸的反射墙。当辐射噪音的扬声器激发两堵墙之间的空间时，这个墙-空气-墙系统在频率为f₁ = 1,130/2L或565/L的地方表现出共振，其中L = 两堵墙之间的距离，而1,130是声速，单位为ft/sec。基频f₁被认为是两个反射墙之间空间的固有频率，并且它伴随着一系列的模式，每个模式也表现出共振。因此，在频谱中，类似的共振会出现在2f₁、3f₁、4f₁等处。对于这种共振，已经有许多不同的名称，包括驻波、房间共振、特征音、允许频率、固有频率或简单地说是模式。通过增加另外两对相互垂直的墙，形成一个矩形的封闭空间，我们还添加了另外两个共振系统，每个系统都有自己的基频和模式系列。

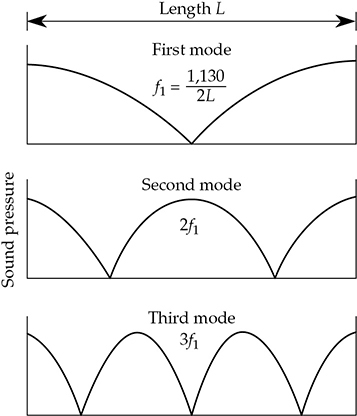
图13-4 两堵平行的反射墙之间的空间可以被视为一个具有共振频率f₁ = 1,130/2L的共振系统。该系统在f₁的整数倍处也表现出共振。

实际上，情况要复杂得多。到目前为止，只讨论了轴向模式，其中每个矩形房间都有三个，以及每个的模式系列。轴向模式反射自两个相对且平行的墙面，切向模式反射自四个墙面，而斜向模式则反射自所有六个表面。如果轴向模式被引用为0 dB级别，则切向模式绘制在-3 dB，斜向模式在-6 dB。在实际应用中，墙面会极大地影响任何特定模式中的实际能量。这三种类型的模式在图13-5中显示。

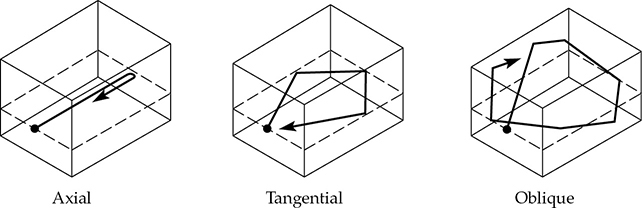
图13-5 利用射线概念可视化轴向、切向和斜向房间模式。

这些模式图提供了清晰的视觉效果，但缺乏严密性。在这些图表中，声音的射线被描绘为遵循入射角等于反射角的法则。对于较高的音频频率，这种射线概念是非常有用的。然而，当封闭空间的尺寸与声音的波长相当时，问题就会出现，射线方法就会崩溃。例如，一个长度为30英尺的录音室在50 Hz时只有1.3个波长长。在这种情况下，射线失去了所有的意义。为了研究更长波长声音的行为，采用了波动方法。

频率区域

在波长的角度来看，听觉频谱非常宽广。在16 Hz处，通常被认为是人耳的低频限制，波长为1,130/16 = 70.6英尺。在听觉上限，通常被引用为20 kHz，波长只有1,130/20,000 = 0.056英尺或约0.7英寸。声音的行为受到声波波长与遇到的物体大小的比较的极大影响。在一个房间里，波长为0.7英寸的声音会被几英寸的墙面不规则性显著地散射（扩散）。相同不规则性对于波长为70英尺的声音的影响将微不足道。声学问题的核心在于，没有一种单一的分析方法可以覆盖如此宽范围波长的声音。

在考虑小房间的声学时，可以将听觉频谱任意分为四个区域：A、B、C和D，如图13-6所示。房间尺寸决定了听觉频谱在声学分析中必须如何划分。在非常小的房间中，由于模态共振过于稀疏，间距太远，可听频谱的大部分被模态共振所主导。

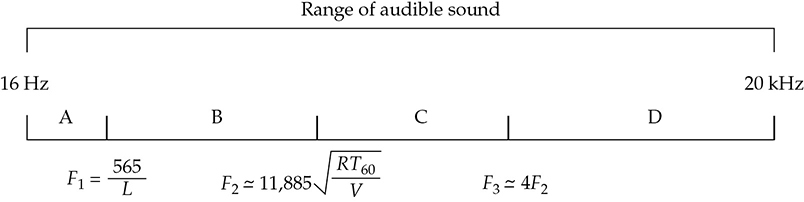
图13-6 处理封闭空间声学时，方便将听觉频率范围分为四个区域：A、B、C和D，由频率F₁、F₂和F₃界定。在A区域中，声音没有模态增强。在B区域，房间模式占主导地位。C区域是一个过渡区，在这个区域中，衍射和扩散占主导地位。在D区域，镜面反射和射线声学占主导地位。

A区域是频率低于1,130/2L或565/L的非常低频区域，其中L是房间的最长尺寸。在这个最低轴向模态频率以下，房间中的声音没有共振支持。这并不意味着这种非常低频的声音不能存在于房间中，只是在该区域内没有模态共振因为那里没有共振。

B区域是房间尺寸与所考虑的声音波长可比较的区域。它的低频端由最低轴向模态，565/L界定。上界并不明确，但可以从以下方程获得其近似值，该方程被称为房间各向同性吸声体的截止或交叉频率：

其中 F₂ = 截止或交叉频率，Hz

 RT₆₀ = 房间的混响时间，秒

      V = 房间体积，ft³

注意：在某些文献中，常数被给定为11,250。

C区域是介于B区域和D区域之间的过渡区域，其中必须使用波动声学，而在D区域，射线声学是有效的。它在低频端近似由截止频率F₂确定，在高频端近似由F₃ = 4F₂确定。这个区域更难分析，主导的波长通常对于射线声学来说太长，对于波动声学来说又太短。

D区域描述了高于F₃的光谱区域，涵盖更高频的可听频率，具有较短的波长；几何射线声学适用。镜面反射（入射角等于反射角）和声音射线方法在这个区域占主导地位。在这个区域通常可以使用统计方法。

总结一下，举例来说，考虑一个尺寸为23.3 × 16 × 10英尺的房间。体积为3,728 ft³，混响时间为0.5秒。A区域在24.2 Hz以下，即565/23.3。对于声音没有模态增强。B区域在24.2到130 Hz之间。使用模态共振的波动声学方法来预测响应。C区域在130 Hz到（4）（130）= 520 Hz之间。这是一个过渡区域。D区域在520 Hz以上。模态密度非常高，通常情况下统计条件占主导地位，可以使用几何射线声学。

房间模式方程式

可以使用波动方程的解来计算矩形封闭空间的房间模式频率。所使用的几何形状如图13-7所示，将三维空间的熟悉的相互垂直的x、y、z坐标适应到一个房间中。为方便起见，将最长的尺寸L（房间的长度）放在x轴上，将次长的尺寸W（宽度）放在y轴上，将最小的尺寸H（高度）放在z轴上。目标是计算矩形封闭空间的模态频率。我们使用Rayleigh首次提出的房间模式方程：

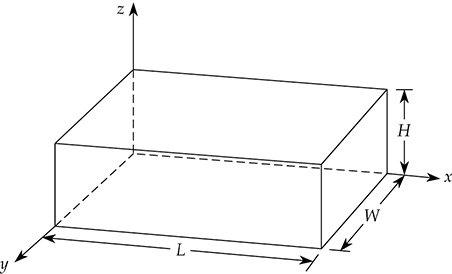
图13-7 计算房间模式频率的矩形房间的定位，其长度L，宽度W和高度H与x，y和z坐标相关。

其中 L，W，H = 房间长度、宽度和高度，以英尺或米为单位

        p，q，r = 整数 0、1、2、3、……

                c = 声速，1,130英尺/秒或344米/秒

这个方程给出了矩形房间的每一个轴向、切向和斜向模式的频率。一旦为给定的房间设定了L，W和H，整数p，q和r就是唯一的变量。只有当p，q和r是整数（或零）时，房间模式才是可能的，因为这是产生驻波的条件。当引入基频（与1相关联）、第二模式（与2相关联）和第三模式（与3相关联）等时，有许多整数的组合。

这些整数用于标识模式是轴向、切向还是斜向，并且还标识给定模式的频率。轴向模式有两个零项，例如（1, 0, 0）或（0, 0, 3）；切向模式有一个零项，例如（1, 1, 0）或（0, 3, 3）；斜向模式没有零项，例如（1, 1, 1）或（3, 3, 3）。此外，模式号表示频率倍数。例如，轴向模式（0, 2, 0）和（0, 0, 2）是（0, 1, 0）和（0, 0, 1）模式的倍数；它们的频率是两倍。同样，更高的整数值描述基本模式的更高倍数。切向和斜向模式的描述方式相同。

如果p = 1，q = 0，r = 0（1, 0, 0模式），宽度和高度项将消失，方程变为：

这是与房间长度对应的轴向模式。我们观察到它与封闭管道的模式方程相同。通过替换适当的尺寸，可以类似地计算宽度轴向模式（0, 1, 0）和高度轴向模式（0, 0, 1）。

房间的相对尺寸决定了模态响应和尺寸的适用性。如果矩形房间有两个或三个尺寸相等或是彼此的倍数，模态频率将重合，在这些频率上会出现峰值，而在其他频率上会出现波谷。例如，如果一个房间的尺寸是10 × 20 × 30英尺（高度、宽度、长度），房间的所有三个轴将在56.5、113、169.5、226、282.5、339 Hz等频率处都有模态频率。这些重合频率称为退化频率，将导致房间频率响应不良且能量分布不均匀。正如我们将看到的，通过精心选择房间尺寸比例，可以极大地改善模态响应。在这种情况下，我们可以看到房间尺寸比例为1:2:3是一个糟糕的选择。

模式计算——一个例子

通过一个例子，最好展示房间模式方程（式13-3）的实用性。房间的尺寸是：长度L = 12.46英尺，宽度W = 11.42英尺，平均高度H = 7.90英尺。（实际上，天花板沿房间长度倾斜，一端的高度为7.13英尺，另一端为8.67英尺。）将L，W和H的值插入模式方程，以及整数p，q和r的组合。注意，该房间不是一个矩形平行六面体，这是房间模式方程的基础。在以下计算中，使用了平均天花板高度；在实践中，这将在结果中引入一些误差。

表13-1列出了这个例子房间的一些模式，按频率升序排列。它显示了每个组合的p，q和r以及由此产生的模态频率。此外，每个频率都通过该p，q和r组合中的零的数量被识别为轴向、切向或斜向。最低的自然房间频率是45.3赫兹，是（1, 0, 0）轴向模式，与房间最长的尺寸，长度L相关，在这以下声音没有模态增强。模式7是（2, 0, 0）模式，是与长度L相关的第二轴向模式，产生90.7赫兹的频率。以相同的方式，模式17是（3, 0, 0）模式，是与长度L相关的第三轴向模式，模式36是第四模式，依此类推。

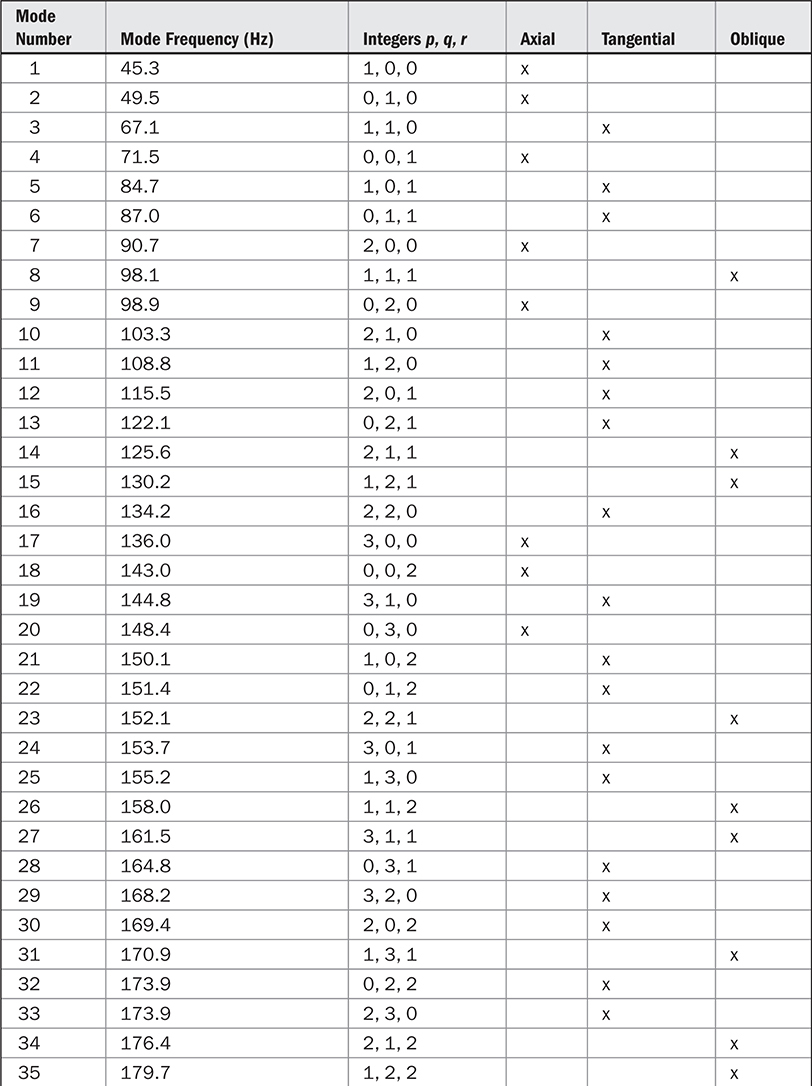
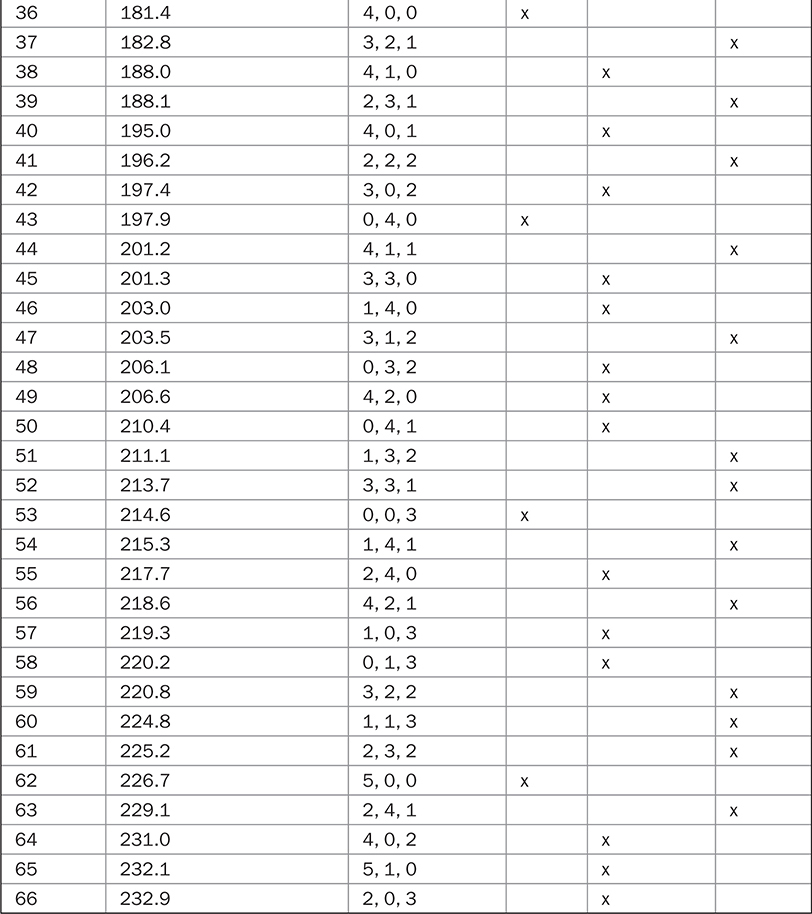
表13-1 模式计算（房间尺寸：12.46 × 11.42 × 7.90英尺）

轴向模式及其间隔已在工作室设计中受到详细研究。轴向模式之间的较大间隙可能导致不均匀的低频响应。然而，房间声学不仅仅是轴向模式。正如表13-1所示，轴向模态频率之间有许多切向和斜向模式，虽然较弱，但也产生影响。

房间模式绝对不只是理论上的奇观。事实上，它们在房间的低频响应中起着主导作用，在那里模式在频率上更为孤立，因此更容易听到。很容易证明它们的深远影响。如果通过扬声器播放模态频率（例如，在这个例子中的136赫兹正弦波），并且听者在房间中走动，那么响亮的反节点和柔和的节点将在房间长度的不同位置清晰可听。根据模式的不同，音调响度的升降可能在房间的长度、宽度或高度上听到，或者是这些因素的组合。另外，如果听者坐在一个地方，并且使用正弦波发生器扫过低频范围，即使扬声器的响应是平坦的，由于房间模式，将在不同的频率上听到巨大的电平变化。此外，坐在另一个位置的听者将听到不同的响应。

想象一下，如果一个声源放置在一个节点上，它只会弱弱地发出那个频率。或者，想象一下一个坐在一个反节点上的混音工程师；由于房间模式的存在，特定频率的响度会被突出显示。房间模式可以极大地影响房间的低频响应，具体取决于声源和接收器在房间中的物理位置。

实验验证

列在表13-1中的模态频率在指定的频率范围内主要决定了这个特定房间的响应。为了评估它们的相对效应，进行了一项扫描正弦波传输实验。实际上，这测量了房间的频率响应。知道所有房间模式终止于房间的角落，一个扬声器（JBL 2135）被放置在房间的一个低三角角落，而测量麦克风则被放置在对角的高三角角落。然后通过缓慢扫描的正弦波信号激发扬声器，扫描范围从10赫兹到250赫兹。记录了麦克风在该信号下的房间响应。得到的追踪结果如图13-8所示。

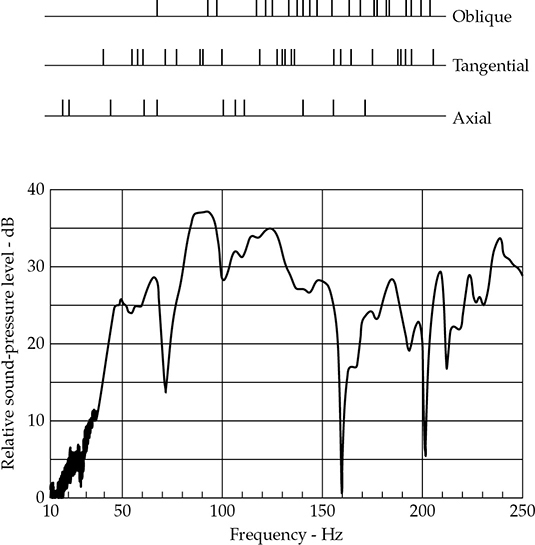
FIGURE 13-8 在表13-1的测试房间中进行的扫描正弦波传输实验。指示了每个轴向、切向和斜向模态频率的位置。

已经尝试识别在所有六个表面均为坚硬和反射的混响室中每个模式的影响。在这种情况下，显著的模式将显现为尖锐的峰值。图13-8所做的录音实际上不是一个混响室。墙壁不是混凝土，而是框架结构，覆盖有石膏板（石膏板）；地板由胶合板铺成，几乎覆盖了一面墙的门。有一个大窗户，墙上有画，还有一些家具。显然，这是一个相当吸声的房间。在125赫兹时的混响时间为0.33秒。这个房间在声学上更接近工作室和控制室，而不是混响室，这就是为什么选择它的原因。

在45.3至232.9赫兹的响应中有12个轴向模式，32个切向模式和22个斜向模式，而这个范围内的房间响应是所有66个模式的复合效应。仅使用图13-8，试图将实验获得的房间响应的峰值和谷值与特定的轴向、切向和斜向模式相对应可能会令人失望。响应可以归因于模式和模式的相互作用；例如，如果相位相位，相邻的模式将预期加强房间响应，如果相位不同，则会取消。实际上，正如我们将看到的那样，需要进行更深入的分析才能完全了解模态房间响应。

三个主要的低谷是如此狭窄，以至于它们对于分布式语音或音乐频谱的能量贡献很小。如果忽略它们，剩下的波动就更为适度。在这种稳态扫描正弦波传输测试中，这种幅度的波动是即使在精心设计的工作室、控制室和听音室中也是特征性的。耳朵通常接受这种对平坦响应的偏差。到目前为止，空间的模态结构总是引起这些种类的波动。然而，声学性能还有更多方面需要考虑，不仅仅是迄今为止考虑的稳态响应。

模态衰减

仅从图13-8的稳态响应中无法完全了解情况。耳朵对瞬态效应非常敏感，而语音和音乐几乎完全由瞬态组成。混响衰减是一种易于测量的瞬态现象。当语音或音乐等宽带声音激发房间的模态时，我们关注的是模态的衰减。45.3到232.9赫兹频带中的66个模态形成了该范围内房间混响的微观结构。混响通常以八度带进行测量，感兴趣的八度带宽度显示在表13-2中。

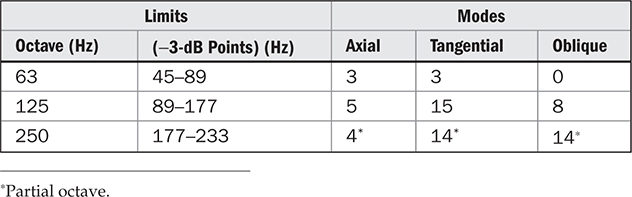
TABLE 13-2 八度带中的模态

因此，每个八度带的混响衰减涉及许多模态的平均衰减，但要解释声音的八度带衰减，需要了解单个模态的衰减。八度中心频率越高，包含的模态数量越多。

不同模态的衰减速度不同。模态衰减取决于吸收材料在房间中的分布方式，等等。放在测试房间地板上的地毯对仅涉及墙壁的(1, 0, 0)或(0, 1, 0)轴模态没有影响。涉及更多表面的切向和斜向模态的衰减速度预计比仅涉及两个表面的轴模态要快。另一方面，对于声音垂直撞击表面的轴模态而言，吸收要大于斜向和切向模态，后者的入射角通常很小。

使用正弦波激励在测试房间中的混响衰减如图13-9所示。单一显著模态独自衰减产生平滑的对数曲线。240赫兹处的双斜率衰减很有趣，因为早期斜率的低值（0.31秒）可能主要由一个涉及大量吸收的单一模态主导，随后让位于遇到较少吸收的其他模态。

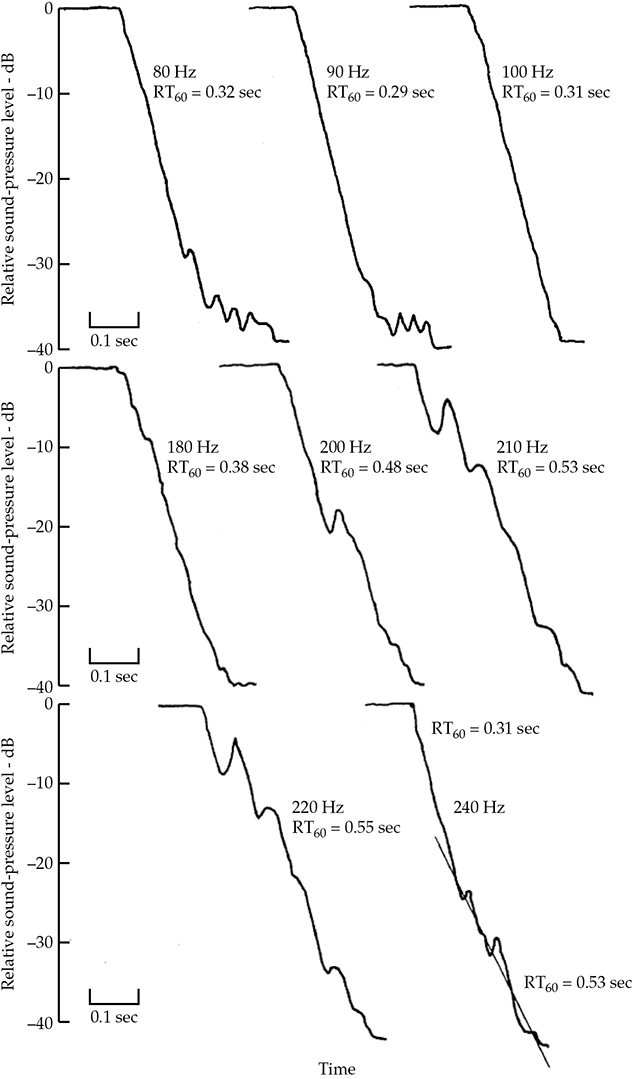
FIGURE 13-9 在测试房间中进行的纯音混响衰减记录。单独衰减的单一模态产生平滑的对数曲线。邻近模态之间的拍子导致不规则的衰减。在前20 dB内，240赫兹处的双斜率模式显示了单一显著模态的平滑衰减，之后一个或多个吸收较少的模态占主导。

从表13-1中识别这些模态是困难的，尽管您可能期望214.6赫兹处的轴模态衰减较慢，而220赫兹附近的模态群被高度阻尼。通常会强制附近的模态振荡，然后以其自然频率衰减。

图13-10显示了使用粉红噪声的八度带测量。125赫兹八度带的衰减（0.33秒）和250赫兹八度带的衰减（0.37秒）平均了许多模态，应被视为该频率区域的“真实”值。然而，通常会对每个频带进行多次衰减以提供统计意义。该房间的测得混响时间总结在表13-3中。

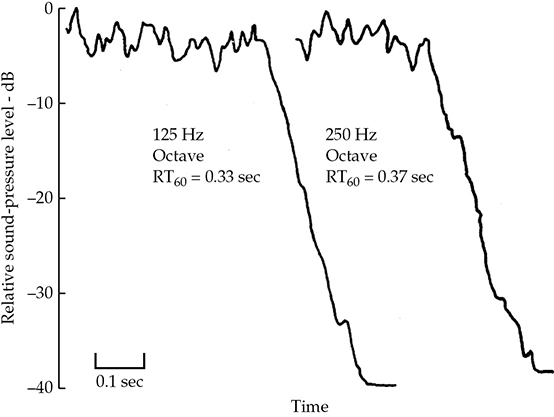
FIGURE 13-10 在测试房间中进行的八度带粉红噪声混响衰减记录。125和250赫兹八度带的衰减显示了这些八度带中所有模态的平均衰减。

TABLE 13-3 测试房间的测得混响时间

模态带宽

正常模态决定了房间的共振频率。单独看每个正常模态都表现为共振曲线，如图13-11所示。带宽定义为共振峰两侧的半功率（–3dB）点。每个模态的带宽由以下表达式确定：

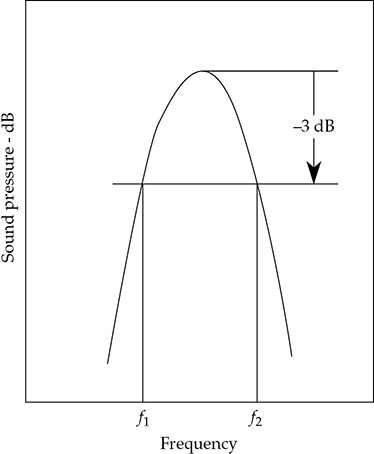
FIGURE 13-11 每个房间模态都有有限的带宽。带宽通常在–3dB点处测量。房间的吸收越多，带宽越大。

其中f₂和f₁是–3dB处的频率，单位赫兹

RT₆₀ = 混响时间，单位秒

带宽与混响时间成反比。房间越沉闷，共振曲线的带宽越宽。在电路中，调谐曲线的陡峭度取决于电路中的电阻量；电阻越大，调谐曲线越宽。在室内声学中，混响时间取决于吸收（电阻）。这个类比是合适的（吸收越多，混响时间越短，模态共振越宽）。为了方便参考，表13-4列出了与混响时间相关的一些带宽值。

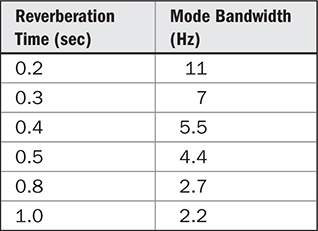
TABLE 13-4 模态带宽

图13-12显示了图13-8的40到100赫兹部分的扩展版本。在此范围内的来自表13-1的轴模态以–3dB点处的6赫兹带宽绘制。轴模态在零参考级别处呈峰值。切向模态的能量仅为轴模态的一半，因此它们的峰值绘制在轴模态的下方3dB（10 log 0.5）。斜向模态的能量仅为轴模态的四分之一，因此在此范围内的唯一斜向模态（98.1赫兹）的峰值绘制在轴模态峰值的下方6dB（10 log 0.25）。

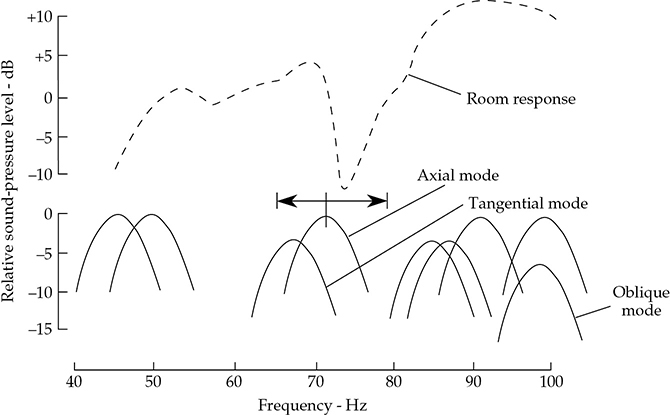
FIGURE 13-12 测得的扫描正弦响应与测试房间计算模态的相关性。显示了图13-8中40到100赫兹范围的房间响应。轴向、切向和斜向模态都被绘制了出来。

典型房间的模态带宽约为5赫兹。这意味着对于混响时间较短的房间，相邻模态往往会重叠，这是理想的。当相邻模态的共振曲线的裙摆重叠时（例如图13-12中标记的轴向和切向模态），通过在其共振频率处驱动房间来激发一个模态也会倾向于迫使另一个模态激发。当第一个激发频率移除时，存储在另一个模态中的能量将以其自身的频率衰减。在衰减过程中，两者将彼此产生拍频。在图13-9中80、90和100赫兹模态等非常均匀的衰减可能是足够远离邻近模态以独立运作而不受拍频干扰。

测试房间的整体响应（在图13-12中标记）最有可能由表13-1中列出的各种模态的集体贡献构成。在这个频率范围内，响应是否可以由轴向和切向模态以及单个斜向模态的集体贡献解释呢？似乎合理的是，通过这个频率范围内的两个轴向、两个切向和一个斜向模态的联合效应来解释房间响应在80到100赫兹之间的12dB峰值。50赫兹以下的下降无疑是由扬声器的响应引起的。这留下了74赫兹处的12dB低谷尚待解释。

71.5赫兹处的轴向模态是测试房间带有倾斜天花板的垂直模态。与平均高度相对应的频率是71.5赫兹，但与天花板低端高度相对应的频率是79.3赫兹，高端高度相对应的频率是65.2赫兹。上面的双箭头表示这个模态频率的不确定性（在图13-12中标记）。如果这个不确定的轴向模态被稍微降低到一个略低的频率，就可以更好地解释响应中的12dB低谷。似乎在60赫兹附近应该出现响应的低谷，但并未找到。

尽管这个测试房间在实验证实了许多房间模态理论的方面，更重要的是，它展示了一些实用的教训。测试房间不是一个矩形平行六面体，这是模态方程的假设基础。此外，在将各个模态的效应结合以获得总体响应时，必须考虑相位。这些组件必须以矢量方式组合，同时考虑幅度和相位。最后，也很重要的是，每个模态不是一个固定的实体，而是一个其幅度从零到最大变化的实体，这取决于房间中的位置。各个压力图在房间内各处变化，不可能通过简单地将所有模态相加来确定房间中某一点的总幅度。例如，在任何点，一个模态可能是零或最大值。房间响应应被视为分布在房间物理尺寸上的组合模态响应，将在以下讨论。

模态压力分布图

房间的模态模式产生了非常复杂的声场。为了说明这一点，展示了几幅声压分布的草图。可以将图13-1的一维风琴管与图13-13中的三维房间的（1, 0, 0）轴向模态进行比较。声压在末端附近较高（1.0），沿着房间中心为零。当只激发（3, 0, 0）轴向模态时，图13-14显示了声压分布。在这种情况下，声压的节点和反节点是图13-15所示的直线。

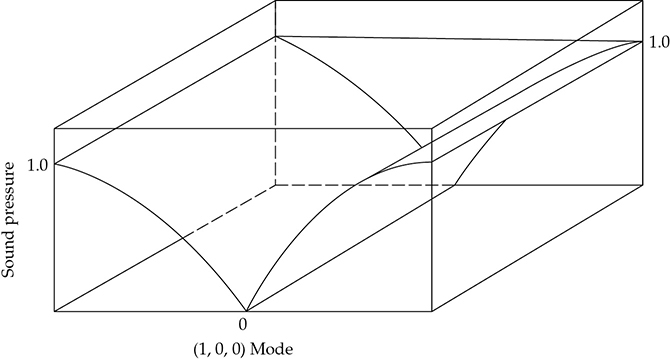
FIGURE 13-13 表示房间（1, 0, 0）轴向模态的声压分布。声压在房间中心的垂直平面上为零，在房间末端最大。这可与图13-1的封闭管的f₁进行比较。

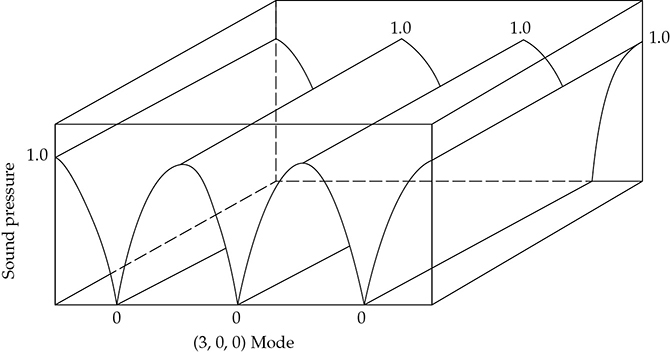
FIGURE 13-14 表示房间（3, 0, 0）轴向模态的声压分布。

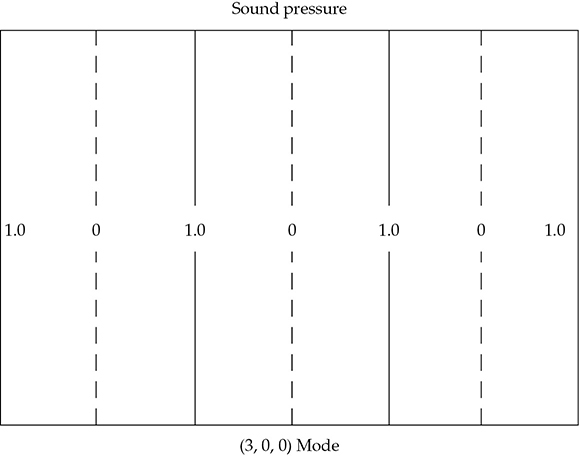
FIGURE 13-15 通过矩形房间截面上的（3, 0, 0）轴向模态的声压等高线。

在更高的模态中，整个房间内声压分布的三维草图变得困难，但图13-16试图展示（2, 1, 0）切向模态。我们看到房间每个角落的声压最大值，中央边缘有两个额外的最大值。在图13-17中，这在地形上被描绘出来，显示了压力等高线。在声音最大值之间交叉的断线标记了零压力区域。

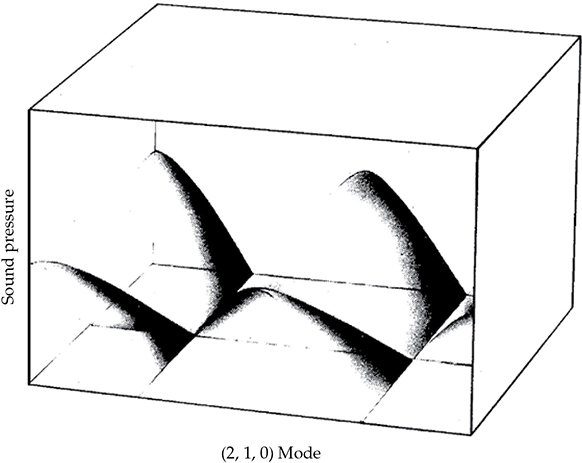
FIGURE 13-16 矩形房间（2, 1, 0）切向模态的声压分布的三维表示。(Brüel & Kjaer Instruments, Inc.)

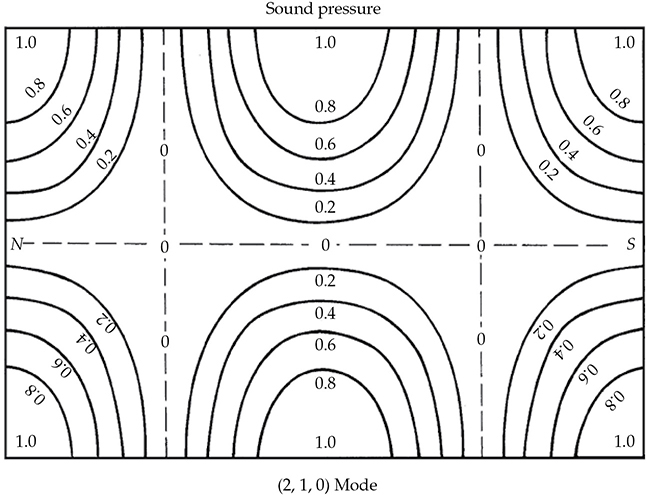
FIGURE 13-17 矩形房间（2, 1, 0）切向模态的声压等高线。

想象一下，如果所有模态都同时或依次由声音或音乐能量激发，而同时不断在频谱中上下移动并不断变化强度，声压模式会变得多么复杂。图13-17的图表显示房间角落的声压最大值。这些最大值在所有模式中始终出现在房间的角落。为了激发所有模态，将声源放在一个角落。反之，如果希望测量所有模态，麦克风应放置在一个角落。

模态密度

模态密度随频率增加而增加。例如，在表13-1中，从45到89赫兹的一个八度内，只有6个模态频率。在下一个更高的八度中有28个模态。即使在这个非常有限的低频范围（200赫兹以下），我们也可以看到模态密度随频率增加。如图13-18所示，随着频率的提高，增加的速率急剧上升。在大约300赫兹以上，模态间距如此之小，以至于房间响应随频率明显平滑。以下方程可用于确定给定中心频率处给定带宽内的模态数量的近似值：

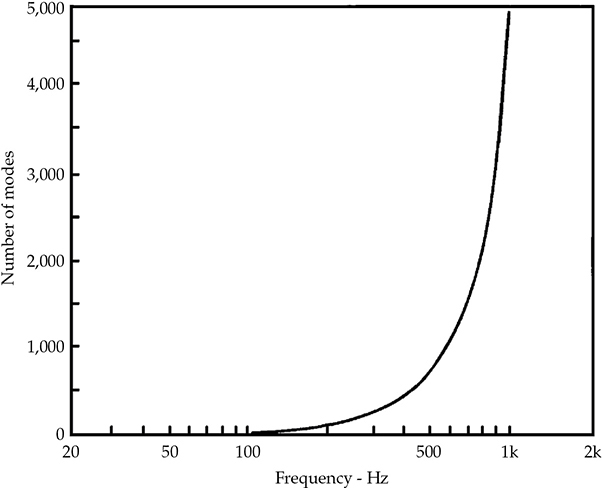
FIGURE 13-18 模态频率随频率增加。

其中 ΔN = 模态数量

       Δf = 带宽，赫兹

         f = 中心频率，赫兹

        V = (l_xl_yl_z) = 房间体积，立方英尺

         S = 2(l_xl_y + l_yl_z + l_xl_z) = 房间表面积，平方英尺

        L = 4(l_x + l_y + l_z) = 房间所有边的长度，英尺

        c = 声速 = 1,130英尺/秒

该方程显示在给定带宽下，模态密度随频率增加。类似地，随着房间尺寸的增加，模态密度也会增加。

在模态密度较低的较小房间中，房间模式最为重要；这尤其发生在低频。在大房间中，模态密度相对较高，除了极低频率之外，房间模式的作用较小。可以用Schroeder方程估算小房间和大房间之间的截止频率：

其中 f_c = 截止频率，赫兹

RT₆₀ = 混响时间，秒

     V = 房间体积，立方英尺或立方米

注：在公制单位中，将11,885更改为2,000。

模态间距与音质缺陷

音质缺陷是音频信号中的频率响应异常，有可能是可听的。它们可以影响任何对声学敏感的空间的声音质量，从听音室到音乐厅都包括在内。任务是确定房间中的数百个模态频率中的哪些可能导致可听的缺陷。

音质缺陷可能导致录音或其他关键工作的质量不佳。一个音高落在相隔很远的模态之间可能异常弱，并且可能比其他音符衰减得更快。从某种意义上说，就好像那个特定的音符是在户外发出的，而其他音符是在室内同时发出的。

模态频率的间距是一个至关重要的因素。在图13-6的D区域中，小房间的模态频率之间的距离如此接近，以至于它们倾向于有帮助且无害地合并。在B和C区域，大约在300赫兹以下，它们的分离更大，正是在这个区域问题可能出现。为了避免音质缺陷，模式不应该被彼此隔离，但它们也不应该彼此重叠。

在模态频率之间允许多少间隔才会出现音质缺陷？Gilford认为，相隔超过20赫兹的轴向模式在声学上往往会被孤立。它们往往不会通过由于重叠的尾巴而导致的耦合而被激发，而是往往会独立地发挥作用。在这种孤立的状态下，它可以对接近其自身频率的信号部分做出响应，并为该部分提供其比例谐振增强，从而潜在地产生音质缺陷。

Gilford的主要关注点是，广泛的轴向模式间隔可能会导致由于独立和未耦合的模态行为而引起的频率响应偏差。Bonello提出了模式间隔的另一个标准。他分析了模式之间的分离以避免退化（重合）效应。在这种类型的分析中，一定程度的分离是可取的。此外，他考虑了所有三种类型的模式，而不仅仅是轴向模式。他指出，最好是使临界带中的所有模态频率之间的间隔至少达到其频率的5%。例如，20赫兹的一个模态频率和21赫兹的另一个模态频率可能勉强可以接受。然而，在40赫兹处，相似的1赫兹间隔将不被接受（40赫兹的5%是2赫兹）。

模态频率之间的零间隔是频率响应偏差的常见来源。零间隔意味着两个模态频率是重合的，这种退化倾向于过分强调该频率的信号成分。模式不应该彼此分隔很远，但它们也不应该彼此重叠。

音质缺陷的可听性

任何耳朵都可能受到由于孤立或增强的模式引起的音质缺陷的侵害，但即使训练有素的耳朵也需要一些仪器辅助来识别和评估这种响应偏差。在BBC研究部门的一项研究中，观察员听取了在研究中的录音室中对麦克风说话的人的声音，声音在另一个房间通过高质量的播放系统进行复制。观察员的判断得到了有选择性地放大狭窄频段（10赫兹）的帮助，使其水平比谱中其他部分高出约25分贝。输出与原始信号混合在一起传递到扬声器，所调整的比例使其几乎不可察觉地成为整个输出的一部分。然后，当选择性放大器调谐到适当的频率时，任何频率响应偏差都变得清晰可听。

在这种方式测试的大多数录音室中，每个录音室通常只发现一个或两个明显的音质缺陷。图13-19是在2年内观察到的61个男性声音的可听音质缺陷的图。大多数发生在100到175赫兹之间。女声的响应变化最常见在200到300赫兹之间。

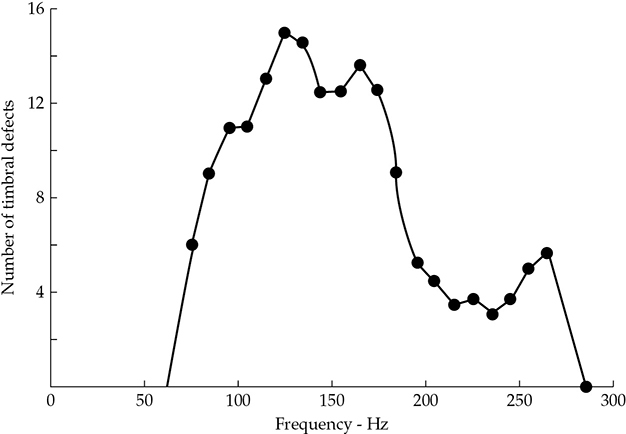
FIGURE 13-19 在BBC录音室中，在2年内观察到的61个男性声音中，可听到的音质缺陷的图。大多数发生在100到175赫兹之间。女声的响应变化最常见在200到300赫兹之间。（Gilford.）

最佳房间比例

房间的比例能否被设计成在整个房间实现最佳的模态分布？这个问题得到了很多强烈的观点的回答——其中一些观点得到了相当令人信服的实验证明，而另一些观点同样强烈，但缺乏很多支持。

房间几何形状极大地影响声学性能。矩形房间的普遍存在主要是由于施工的经济性，但这种几何形状具有声学优势。轴向、切向和斜向模式可以轻松计算，并且它们的分布可以进行研究。作为第一次近似，一个好的方法是仅考虑较为显著的轴向模式。可以识别退化模式并揭示其他房间缺陷。

对声学敏感房间的长度、宽度和高度进行相对比例是一个重要的考虑因素。当为这样的房间绘制平面图时，应该从基本的房间比例开始。立方形房间是可憎的，因为它们的模态分布很差。

文献中包含了早期的准科学猜测，以及后来对产生良好模态分布的房间比例进行的统计分析。Bolt提供了在小矩形房间中产生低频平滑房间特性的房间比例范围。Volkmann的2:3:5比例有时会被使用。Boner建议使用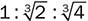（或1:1.26:1.59）比率作为最佳选择。Sepmeyer提出了几个有利的比率。Louden列出了基于1:1.4:1.9比率的125个尺寸比率，并按房间声学质量降序排列。

表13-5总结了这些研究人员建议的一些有利的矩形房间比例。 图13.20在Bolt建议的有利区域的基础上绘制了这些比例。大多数比率都在或非常接近“Bolt区域”。这表明一个落在Bolt区域的比率将在轴向模式频率分布方面产生可接受的低频房间质量。然而，特别是对于小房间，在那里满意的模态响应是最困难的，任何提议的比率都必须经过测试。Bolt规范的有效频率范围因房间体积而异；例如，在一个8,000立方英尺的房间中，有效范围约为20到80赫兹。

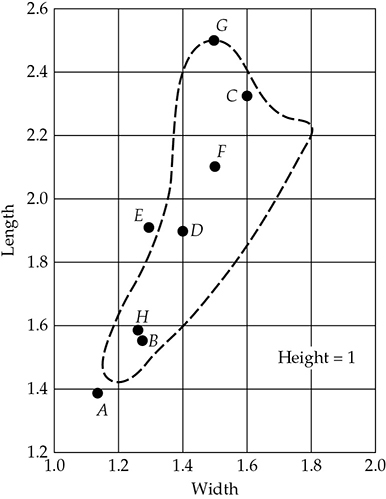
FIGURE 13-20 有利的房间尺寸比例图，以实现房间内模态频率的均匀分布。虚线包围了Bolt区域。Bolt规范的有效频率范围因房间体积而异。字母指的是表13-5。

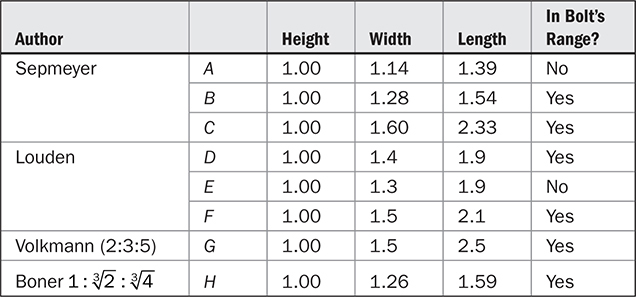
TABLE 13-5有利的模态分布的矩形房间尺寸比例

单凭外观无法判断房间的尺寸比例是否合适；需要进行具体的分析。假设房间高度为10英尺，并选择其他两个尺寸作为有利的比例，可以进行轴向模态分析。房间尺寸比例A到H（来自表13-5）的结果在图13-21中绘制。

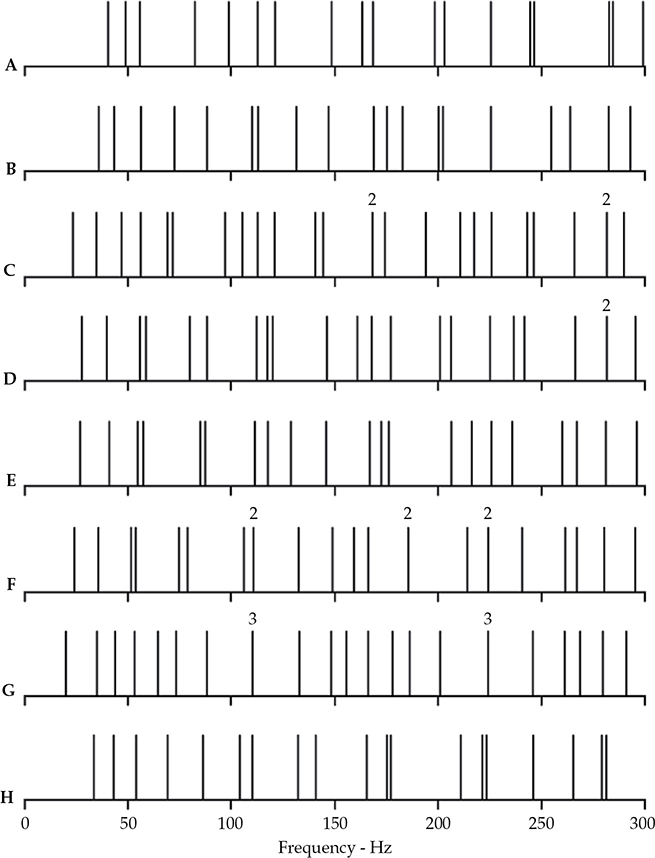
FIGURE 13-21 八个有利房间比例的轴向模态分布图，详见表13-5。数字表示在那些特定频率处重叠的模态数量。假设房间高度为10英尺。

在天花板高度为10英尺的情况下，图13-21中的房间都相对较小。所有小房间都面临轴向模态分离大于期望值的相同问题。间距越均匀，效果越好。在图13-21中通过上面的“2”或“3”上标标识的重叠的谐振频率表示潜在问题。即使没有实际重叠，间距非常接近的模态也可能存在问题。有了这些规则，图13-21中的哪种分布更可取呢？

在这个例子中，我们可能会因为两个三重重叠与相邻模态之间的间隔而拒绝G。由于F有三个双重重叠和一些间隔，我们也可能淘汰它。我们可以忽略C和D中接近280 Hz处的双重重叠的效应，因为很少在200 Hz以上经历频率响应偏差。除了这些保留意见外，很难区分其余的情况。每个都有缺陷，但鉴于我们对潜在问题的警觉，每个都可能表现良好。这种有关模态分布的简单分析只考虑轴向模态，知道较弱的切向和斜交模态只能通过填充较广泛间隔的轴向模态之间来提高效果。这可能会改变我们对特定首选比例的看法。

如果正在建造一个新房间，您可能有自由移动墙壁或提高/降低天花板以改善模态分布。在选择房间尺寸时，一个主要目标是避免轴向模态的重叠。例如，如果分析一个立方体空间，三个基频和所有谐波将会重叠。这会在每个模态频率处产生三重重叠，同时在模态之间产生间隙。毫无疑问，在这样一个立方体空间中的声音在声学上会非常差。相反，房间模态的频率间隔应尽可能均匀。

例如，一个尺寸为19.42英尺长、14.17英尺宽和8英尺高的房间在29.1到290.9 Hz之间有21个轴向模态。如果均匀分布，间距约为13 Hz，但间距在3.2到29.1 Hz之间变化。然而，没有重叠；最接近的轴向模态相隔3.2 Hz。尽管这不能表示为最佳的比例，但经过适当处理，这个房间将从模态的角度产生良好的音质。正确的起点是适当的房间比例。

在改造现有空间时，您可能没有自由改变房间比例。然而，轴向模态的研究仍然可能非常有帮助。例如，如果分析显示一个与相邻模态相隔较远的重叠，那么通过对其影响的了解，就会警告潜在的问题。作为一种解决方案，可以将赫姆霍兹共振器调谐到有问题的重叠频率以控制其效应。或者，如果空间允许，在现有墙壁内放置一堵新的墙壁可能会改善模态分布。

Bonello 法则

在审查各种首选房间比例时，我们已经观察到选择合适的尺寸比例对于获得良好的模态响应至关重要。例如，任意两个尺寸的比例不应是整数或接近整数。Bonello提出了一种确定矩形房间比例声学适宜性的方法。他将可听频谱的低端分为1/3倍频程的频段，并考虑每个频段在200 Hz以下的模态数量。选择1/3倍频程是因为它们近似于人耳的临界带。

为了符合Bonello的标准，每个1/3倍频程的模态数量应比前一个更多，或者至少相同。不允许模态重叠，除非该频段至少有5个模态。一个尺寸为15.4 × 12.8 × 10英尺的房间是否符合这一标准？图13-22显示它通过了测试。图表稳步上升，没有向下的异常。40 Hz处的水平部分是允许的。这表明了良好的模态响应。

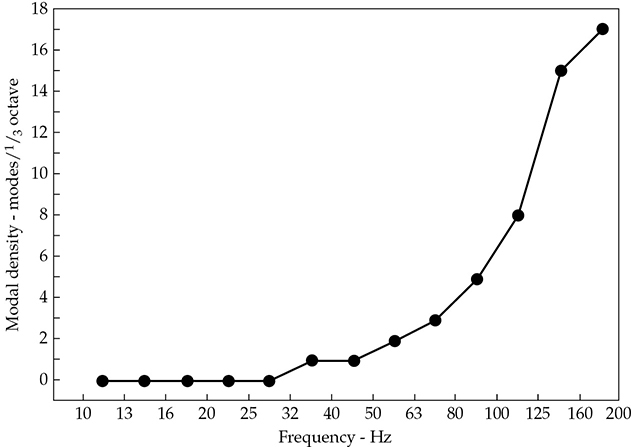
FIGURE 13-22 一个显示尺寸为15.4 × 12.8 × 10英尺的房间1/3倍频程频段中模态数量的图表。图表稳步上升，没有向下的异常；因此，该房间符合Bonello的标准。

尽管许多作者提出了各种用于获得最佳模态响应的房间尺寸比例，但重要的是要记住，没有理想的尺寸比例。此外，追求完美比例是不可能的。在实际房间中，房间在低频时的结构完整性不均匀；在给定的声源位置，各种模态的激发不均等；并且坐着的听众只能听到其中的一些模态。模态响应是一个真正的问题，但使用概括的假设确切地预测响应是非常困难的。换句话说，根据一般性的指导方针和建议，必须根据具体情况考虑每个房间的模态响应。

扩展房间表面

倾斜（斜置）声学敏感房间的一面或两面墙并不能消除模态问题，尽管它可能会在房间中略微移动它们并产生名义上更好的扩散效果。倾斜的墙在新建时可能不会增加成本，但在改建现有空间时可能会相当昂贵。倾斜一对相对的墙壁可以控制混响回声。倾斜的量通常在1:20到1:10之间，例如在20英尺中1英尺和在10英尺中1英尺。在一些录音室控制室设计中，房间的前表面被倾斜，以便将来自监视扬声器的早期反射引导远离混音位置；这种设计有时被称为无反射区。这在第24章中会有更详细的讨论。

非矩形房间

在音频房间中使用非矩形几何形状所产生的声学效益存在争议。正如吉尔福德所指出的，为了避免平行表面，倾斜墙壁并不能消除音色缺陷，但确实使其更难以预测。梯形形状的空间通常用作录音室控制室外壳，尽管普遍认为控制室具有双侧对称性是非常理想的。

基于有限元方法的计算机研究揭示了在非矩形房间中低频声场的情况。由van Nieuwland和Weber进行的一项研究的结果显示在图13-23到13-26中，比较了矩形几何和非矩形几何的情况。非矩形几何的四种模态显示出高度扭曲的声场。所示四种情况中的站立波与相同面积的矩形几何的频率相比发生了变化：分别为-8.6%、-5.4%、-2.8%和+1%。这支持了一种常见说法，即倾斜墙壁在破坏退化性方面略有帮助，但需要5%或更大的偏移才能避免退化性的影响。可以选择矩形房间的比例来消除或至少大大减少退化，而在非矩形房间的情况下，事先检查退化性是困难的。通过倾斜墙壁使声场变得不对称会引入设计的不可预测性。如果决定在房间中倾斜墙壁，比如5%，一个合理的近似方法是分析具有相同体积的等效矩形房间。

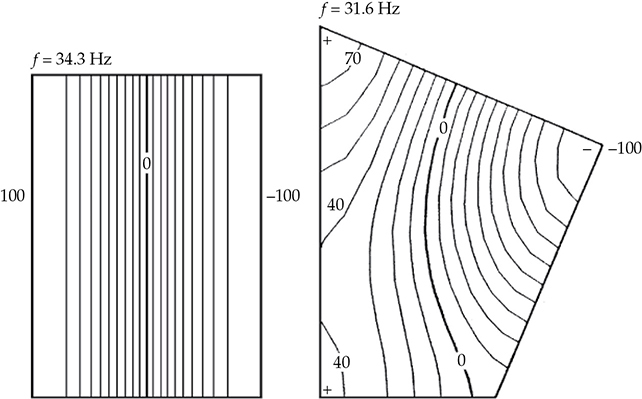
FIGURE 13-23 比较了一个二维矩形房间（尺寸为16.4×23英尺）和相同面积的非矩形房间的模态图案。非矩形房间的（1, 0, 0）模态声场发生了扭曲，并且模态频率略有变化。

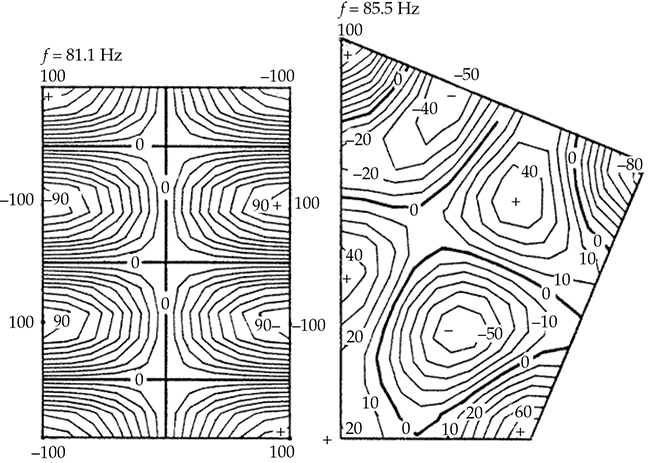
FIGURE 13-24 与图13-23中相同的二维矩形房间和非矩形房间，比较了（1, 3, 0）模态。声场发生了扭曲，并且频率发生了变化。

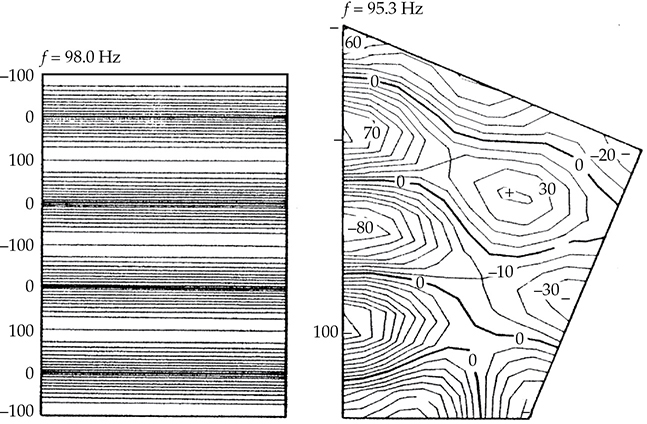
FIGURE 13-25 与图13-23中相同的二维矩形房间和非矩形房间，比较了（0, 4, 0）模态。声场发生了扭曲，并且频率发生了变化。

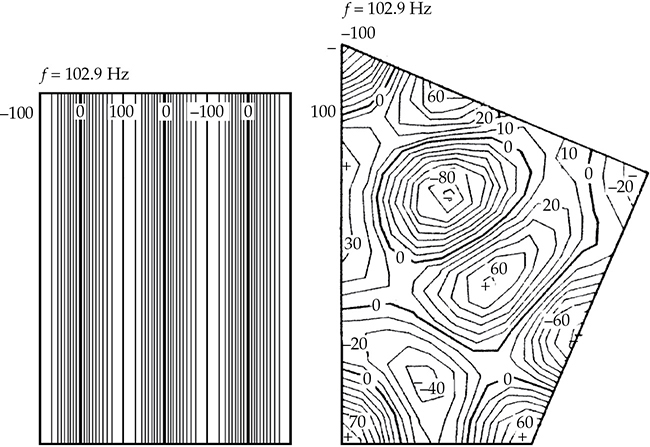
FIGURE 13-26 与图13-23中相同的二维矩形房间和非矩形房间，比较了（3, 0, 0）模态。声场发生了扭曲，并且频率发生了变化。

控制问题模态

正如前文所述，赫姆霍兹共振器是控制房间模态的一种可能解决方案，通过在窄带宽处增加吸收来实现。如果目标是控制一个模态或紧密间隔的模态组，共振器的放置就很重要。假设图13-17的(2, 1, 0)模态正在导致声音质量的音色变化，并且有必要在(2, 1, 0)频率引入窄带吸收。为了最大限度地发挥效果，赫姆霍兹共振器应放置在调谐频率的高模态声压区域。如果将赫姆霍兹共振器放置在压力节点（零压力）处，它几乎不会产生影响。将其放置在其中一个波峰（压力峰值）上，它将与(2, 1, 0)模态发生高度互动。因此，任何一个角都是可以接受的，墙壁上的波峰位置也可以。

制造具有非常尖锐调谐（高Q）的共振器可能是有挑战性的。木箱的弯曲会引入降低Q的损耗。为了获得真正高Q且调谐尖锐的共振器，腔体必须由混凝土、陶瓷或其他坚硬、不屈服的材料制成，并配备一些可变换谐频的手段。

通常难以实现对可听频谱的最低一个或两个八度的声音吸收。录音室控制室通常使用低音陷阱来降低低音频率的房间模态。对于吸收非常低的低音频率，需要较大的陷阱深度。通常使用在控制室天花板上方和内墙与外壳之间的未使用空间作为陷阱空间。

简化轴模分析

总结轴模分析，该方法应用于一个示例房间。房间的尺寸为28 × 16 × 10英尺。28英尺的长度以565/28 = 20.2 Hz共鸣，两个相隔16英尺的侧墙以565/16 = 35.3 Hz共鸣，楼板天花板组合以565/10 = 56.5 Hz共鸣。这三个轴向共鸣及其各自的倍数在图13-27中绘制。在300 Hz以下，有27个轴向共振频率。在此练习中，将忽略较弱的切向和斜向模态。

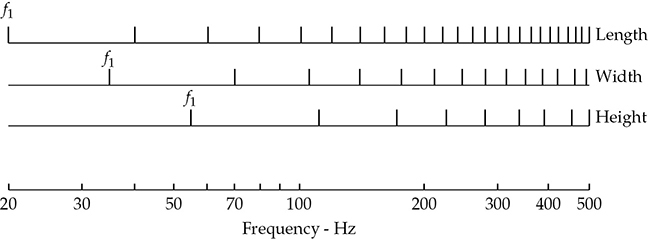
FIGURE 13-27 28 × 16 × 10英尺房间的轴向模频率和倍频。

由于许多音色缺陷可以追溯到轴向模态，因此将详细检查它们的间隔。在表13-6中，以简化的形式呈现了对轴向模态的分析。从第四列中的L、W和H列中提取的共振频率按升序排列。这使得轴向模态间隔的关键因素易于检查。

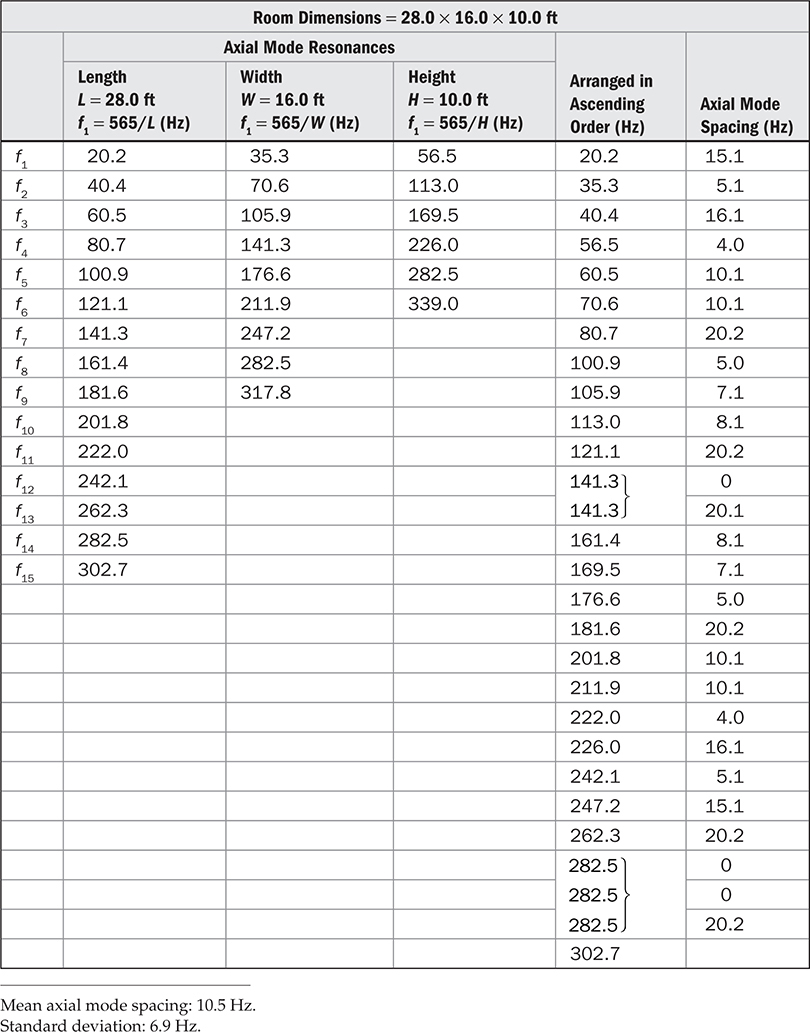
TABLE 13-6 轴向模态的简化分析

在141.3 Hz处，L-f₇共振与W-f₄共振相重叠。这意味着这两个轴向模态可以共同产生该频率的潜在响应偏差。这个巧合还与相邻模式相隔20 Hz。在282.5 Hz处，我们看到L-f₁₄、W-f₈和H-f₅模态的三重简并，它们似乎是音色缺陷的麻烦源。它们与邻居相隔20 Hz。如果这是一个拟议的房间设计，应重新评估房间尺寸以获得更好的模态响应。在现有房间中，一个调谐锐利且位置合适的赫姆霍兹共振器提供了一个可能的解决方案。

要点

• 声学谐振，通常称为正常模式或驻波，在封闭空间中自然存在。它们在整个封闭空间内产生不均匀的能量分布，特别是在大多数房间的低频段。

• 两端封闭的管道模拟了房间中相对表面之间的谐振条件。纵波驻波是以自然模态频率及其倍数产生的。管道的共鸣频率由管道的长度决定。

• 在任何点，粒子位移与声压级完全异相；每个压力反节点处都有一个位移节点，每个位移反节点处都有一个压力节点。例如，封闭管道的两端粒子位移始终为零。

• 尺寸与可听声音波长相当的小房间可能存在模态过度分离的问题。

• 随着频率的增加，模态数量大大增加。在大多数房间中，超过300 Hz，平均模态间距变得非常小，房间响应趋于更加平滑。

• 房间模态方程使用房间的相对尺寸来确定模态响应，从而确定尺寸的适用性。如果矩形房间的两个或三个尺寸相等或是彼此的倍数，将产生重叠的模态频率。

• 重叠的模态频率，称为简并频率，将导致房间频率响应不良，模态之间存在较大的分离。通过仔细选择房间尺寸比例，可以极大改善模态响应。

• 轴向模态包括沿一个轴平行移动的两个相向波，并仅击中两面墙。轴向模态对空间的声学特性产生最突出的贡献。由于矩形房间有三个轴，因此有三个基本轴频率，每个都有自己的模态系列。

• 切向模态包括四个从四面墙反射并平行移动到两面墙的波。切向模态的能量仅为轴向模态的一半，但它们对房间声学的影响可能很显著。每个切向模态都有自己的系列。

• 斜向模态包括八个从封闭空间的所有六面墙反射的波。斜向模态的能量仅为轴向模态的四分之一，不如其他两者突出。

• 由于房间模态，房间低频响应在房间中的不同位置可能会有很大的差异；这对于放置在房间中的声源和接收器都是真实的。

• 为了有效吸收给定模态，吸收材料必须位于模态压力较高的表面。例如，地板上的地毯对水平轴向模式没有影响。切向和斜向模式与轴向模式相比与更多表面反射相关；因此可能有更多的处理位置。

• 轴向、切向和斜向模式的衰减速率不同。因此，每个八度带的模态衰减涉及许多模态的平均衰减。

• 典型房间的模态带宽约为5 Hz。这意味着相邻模式往往会重叠，对于具有短混响时间的房间而言，这是可取的。

• 在给定带宽上，模态密度随频率增加而增加。类似地，随着房间尺寸的增加，模态密度也会增加。

• 为避免音色缺陷，模式不应相互分离得太远，但也不应相互重叠。

• 落入Bolt区域的房间尺寸比例通常会产生可接受的低频响应，就轴向模式频率的分布而言。

• 根据Bonello的标准，每个1/3八度带的模态数量应该比前一个更多，或者至少相同。除非该频带中至少有5个模式，否则不允许模态巧合。

• 倾斜房间的一面或两面并不能消除模态问题，尽管它可能会在房间中轻微移动它们并产生名义上更好的扩散。

• 以确定模态响应是非常困难的。根据一般指南和建议工作，必须逐案考虑每个房间的模态响应。