《声学手册(第七版)》第九章
章节 9
扩散
为了使他们的计算更容易,理论家通常假设完全扩散的声场,即各向同性且均匀的声场。也就是说,在任何点上,声音可以来自任何方向,并且场中的声音在整个房间内都是相同的。然而,在实际情况中,这种完全扩散的情况很少出现,特别是在小房间里。相反,正如我们每天清楚听到的那样,大多数房间内的声音特性显著不同。在某些情况下,定向性是受欢迎的,因为它可以帮助听众定位声音的来源。在大多数房间设计中,扩散被用于更有效地分布声音,并在浸入式声音的同时为房间提供更均衡的响应,同时保持适合应用的定向性水平。由于房间的模态响应,通常很难提供足够的扩散,特别是在低频和小房间中。大多数房间设计的目标是在可听频率范围内获得声能在整个房间内均匀分布。虽然这是不可实现的,但是扩散在这一努力中起到了很大的帮助。
完全扩散声场
尽管完全扩散声场是不可实现的,但考虑其特性对我们具有指导意义。Randall和Ward提出了以下理想条件:
• 稳态测量得到的频率和空间不规则性必须可以忽略。
• 衰减特性中的拍现象必须可以忽略。
• 衰减必须是完全指数的(在对数坐标上将呈现为直线)。
• 混响时间在房间内所有位置都相同。
• 衰减的特性在所有频率上基本相同。
• 衰减的特性与测量麦克风的方向特性无关。
这六个因素是基于观察的。从更理论的角度来看,扩散声场可以用能量密度、能量流以及无限多个平面波的叠加来定义。然而,这六个特性指导我们通过实际方法来判断给定房间内声场的扩散程度。
评估房间内的扩散
为了获得放大器的频率响应,会输入一个可变频率信号并观察输出以测量响应。同样的方法也可以应用于房间的播放系统,通过扬声器重新产生可变频率的信号,并通过位于房间内的麦克风来测量声学信号。然而,房间内播放系统的声学响应从未像电气设备的响应那样平坦。这些偏差部分是由于房间内的非扩散条件。正如前文提到的,扩散是受欢迎的,因为它有助于将听众包围在声场中。另一方面,过多的扩散可能会使定位声源变得困难。
稳态测量
图9-1显示了一个体积为12,000立方英尺的小型工作室的稳态响应。在这个例子中,扬声器放置在房间的一个下部三角区,而麦克风则位于上部对角三角区,距离每个三角区表面约1英尺。选择这些位置是因为所有房间模式都在角落中终止,并且在响应中应该代表所有模式。在从30到250赫兹的线性扫描中,这个响应的波动范围约为35分贝。空波非常狭窄,而狭窄的峰值显示出是单一模式的证据,因为该房间的模式带宽接近4赫兹。较宽的峰值是几个相邻模式的联合效应。从30赫兹到50赫兹的上升主要是由于扬声器的响应,而在50赫兹到150赫兹之间的9分贝峰值是由于扬声器辐射到四分之一空间中。因此,这些是测试中的人工效果,不属于房间响应的一部分。
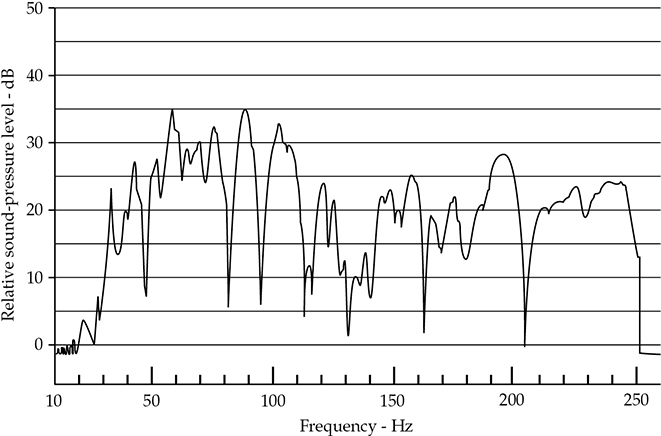
FIGURE 9-1 一个12,000立方英尺工作室的缓慢扫描正弦波声传输响应的录音示波图。许多工作室都具有这种幅度波动,这是非扩散条件的证据。
在图9-1中所示的响应,即使是最好的工作室也是典型的。这样响应的变化是声场不是完全扩散的证据。即使在消音室中进行的这种稳态响应仍然会显示出变化,但幅度会更小。而一个非常多声反射的房间,例如混响室,会显示出更大的变化。
固定测量是获得房间稳态响应的一种方法。评估房间扩散的另一种方法是在保持扬声器频率响应恒定的情况下,将高指向性麦克风在不同平面上旋转,并记录麦克风在恒定激励下的输出。这种方法在大型空间中有一定的成功,但在扩散问题最严重的小房间中不太适用。然而,原则上,在完全均匀的声场中,指向性很强的麦克风指向任何方向都应该接收到一个恒定的信号。固定测量和旋转测量方法都揭示了与真正均匀声场相比的偏差。我们看到,在任何实际的房间中,都不满足频率和空间不规则性可以忽略的标准。
衰减拍
通过参考后面的图11-9,我们可以比较从63赫兹到8千赫兹的八个八度的混响衰减的平滑程度。一般来说,随着频率的增加,衰减的平滑性增加。这是因为,如第13章中所解释的,每个八度范围内的模式数量随频率增加而大大增加,模式密度越大,平均效果越平滑。相反,在这个例子中,63赫兹和125赫兹的衰减中的拍现象最为明显。如果所有频率上的衰减特性都相同,并且这种特性是平滑衰减,那么就实现了完全扩散。在实际情况中,衰减(如图11-9所示)具有显著的特性变化,在63赫兹和125赫兹的衰减中尤其常见。
低频混响衰减中的拍信息使我们能够判断扩散的程度。从图11-9的衰减可以看出,这个特定工作室内声音的扩散程度是通过传统手段所能实现的最好水平。仅提供关于平均斜率而不是衰减形状的混响时间测量设备,忽略了大多数顾问在评估空间的扩散性时认为重要的信息。
指数衰减
真正的指数衰减在水平(对数刻度)与时间图上可以看作是一条直线,而该直线的斜率可以用每秒钟的分贝衰减率或混响时间(以秒为单位)来描述。在图9-2中所示的噪声250赫兹八度带的衰减呈现出两个指数斜率。初始斜率对应混响时间为0.35秒,而最后的斜率对应混响时间为1.22秒。当声级较低时,较慢的衰减可能是由于特定模式或一组模式遇到较低的吸收,可能是因为以斜射角击中吸声材料,或者击中边界处的吸收较少。这是一种非指数衰减的典型情况,或者更准确地说,是一种双指数衰减。
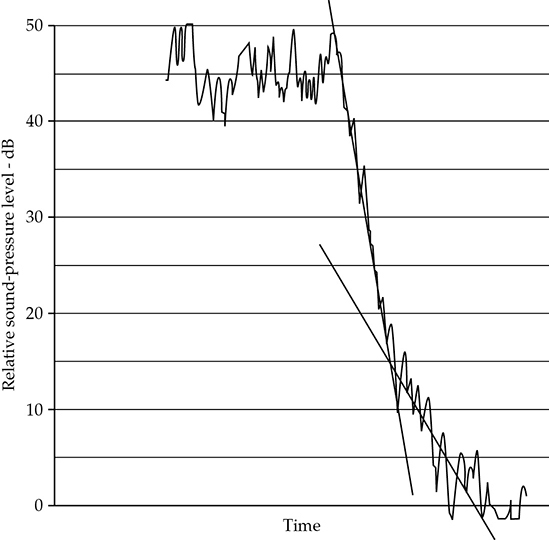
FIGURE 9-2 典型的双斜率衰减,显示了缺乏扩散声条件。较慢衰减的最后阶段可能是由于遇到较低吸收的模式。
另一种非指数衰减类型在图9-3中所示;响应与直线斜率偏离。这是在一个容量为400个座位的教堂内,与相邻房间隔离较差的情况下,对以250赫兹为中心的八度带噪声的衰减。在与声学耦合的空间中进行的衰减测量特点是向上凹(例如在图9-3中),而且偏离直线的程度通常更大。当衰减曲线不是指数形状,即在水平与时间图中偏离直线时,我们可以得出真正的扩散条件并未实现的结论。
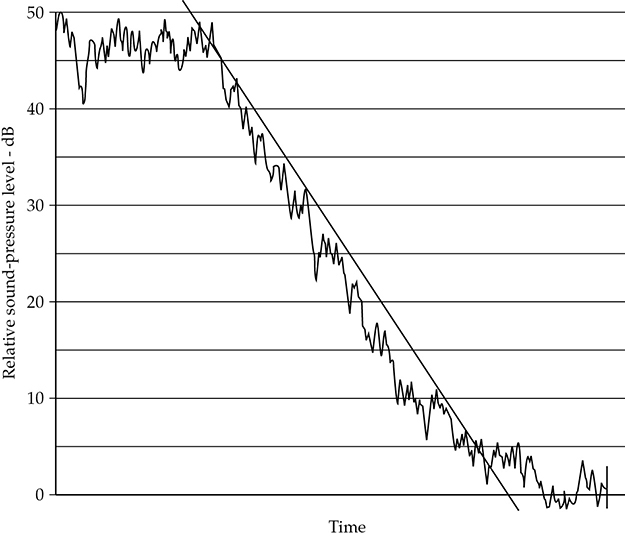
FIGURE 9-3 这种衰减的非指数形式归因于该示例中的声学耦合空间。显示了缺乏扩散声场。
混响时间的空间均匀性
当报告给定频率的混响时间时,最准确的陈述应该是在房间的几个位置进行多次观测的平均值。这可以解释混响条件在房间不同位置不同的事实。图9-4显示了在一个体积为22,000立方英尺的视频工作室进行的测量结果。该空间的多种用途需要可变的混响时间,这通过装有铰链的墙板来实现,可以关闭揭示吸声面,或者打开揭示反射面。在“反射面板”和“吸声面板”条件下,相同的三个麦克风位置记录了多个混响衰减。开放和填充的圆圈分别表示反射和吸声条件的平均值,而实线、虚线和点线表示三个麦克风位置的平均混响时间。显然,有相当大的变化,这意味着在这个瞬态衰减期间,房间的声场并不完全均匀。声场的不均匀性是导致房间内混响时间在不同位置上变化的一个原因,但也有其他因素。对衰减曲线拟合直线的不确定性也有助于数据的扩散,但这个影响应该在不同位置上相对稳定。因此,合理地推断混响时间的空间变化至少部分上与空间中的扩散程度有关。
混响时间的标准偏差为我们提供了在房间的不同位置测量的数据分散程度的见解。当我们计算平均值时,我们会失去数据分散在平均值中的所有证据。标准偏差可以用来量化数据的分散。如果分布是正态(高斯)分布,平均值加减一个标准偏差将包含68%的数据点,而混响时间数据应该相当符合正态分布。 表9-1显示了在图9-4中绘制的视频工作室混响时间的分析结果。对于500赫兹的“反射面板”条件,平均混响时间为0.56秒,标准偏差为0.06秒。对于正态分布,68%的数据点将在0.50秒到0.62秒之间。0.06标准偏差占0.56平均值的11%。 表9-1中列出的百分比给我们提供了对平均值精度的粗略评估。
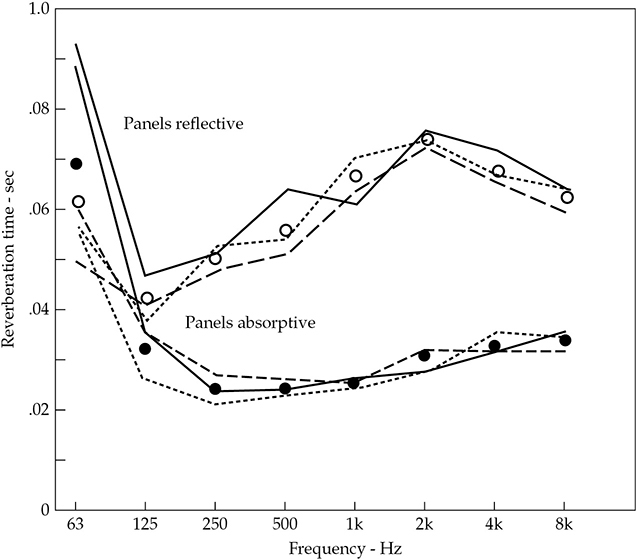
FIGURE 9-4 一间体积为22,000立方英尺的视频工作室混响时间特性,可通过装有铰链的墙板进行调整,一侧为吸声,另一侧为反射。在每个频率下,三个位置的平均混响时间的变化表明存在非扩散的条件。这在低频特别明显。
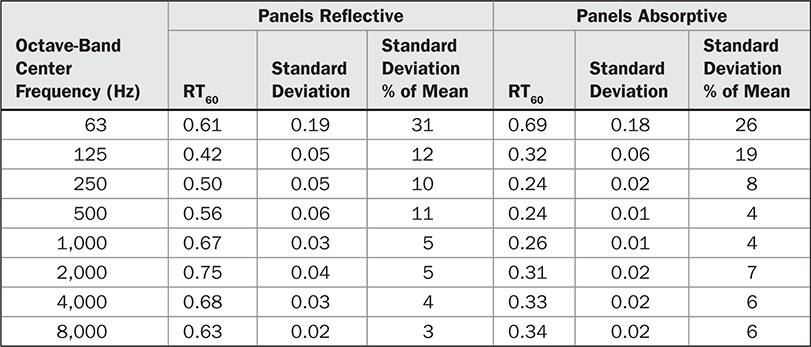
TABLE 9-1 对体积为22,000立方英尺的视频工作室混响时间的分析结果
在表9-1中的百分比列在图9-5中绘制。高频的混响时间值的可变性趋于大约3%到6%的相对稳定值。因为我们知道高频的每个八度包含大量模式,导致平滑衰减,我们可以得出结论,在较高的可听频率下,基本上存在扩散条件,3%到6%的可变性是正常的实验测量变化。然而,在低频下,高百分比(高可变性)是由于更大的模式间距导致的,从一个位置到另一个位置的混响时间产生了相当大的变化。这些高百分比包括拟合低频不均匀衰减特性的直线的不确定性。然而,如图9-4所示,三个测量位置之间的混响时间差异很大。因此,对于这个工作室在两种不同吸声条件(板开/板闭)下,63赫兹的扩散较差,125赫兹稍好,而250赫兹及以上的扩散相当不错。
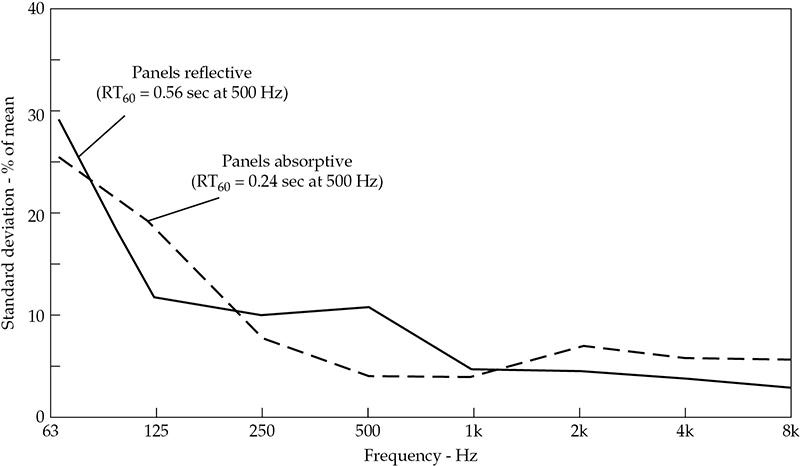
FIGURE 9-5 对表9-1中数据的混响时间变化的图形表示。标准偏差以平均值的百分比表示,显示了缺乏扩散,特别是在250赫兹以下。
几何不规则性
研究人员已经研究了什么类型的墙面凸起可以提供最佳的扩散效果。Somerville和Ward报告称,几何扩散元素减少了扫频稳态传输测试中的波动。他们报告说,这种几何扩散器的深度必须至少为波长的1/7,才能产生效果。他们研究了圆柱形、三角形和矩形元素,并发现矩形形状的扩散器的直边对稳态和瞬态现象的效果最大。其他经验表明,在使用矩形装饰(如穹顶造型)广泛的工作室和音乐厅具有优越的主观声学特性。
局部吸声
在一个房间中将所有吸声材料都放在一个或两个表面上,并不会导致更扩散的条件,也不会最有效地利用吸声材料。考虑一项实验的结果,显示吸声材料分布的效果。这个实验室的大约是一个10英尺的立方体,房间是铺砖的(对于录音或听音室来说并不理想,但对于这个实验是可以接受的)。在测试1中,测量了裸露房间的混响时间,并发现在2千赫兹处为1.65秒。在测试2中,将常见的商业吸声材料应用于其中一个墙面的65%(65平方英尺),在相同频率下的混响时间约为1.02秒。在测试3中,相同面积的吸声材料被分成四个部分,一块放在房间的四个六面体的表面上(三面墙的每面一块,地板上一块)。这将混响时间降低到约0.55秒。
测试2和3中吸声材料的面积是相同的;唯一的区别是在测试3中它被分成了四块。通过简单地将吸声材料分割和分布,混响时间几乎减少了一半。将1.02秒和0.55秒的混响时间值及房间的体积和面积插入Sabine方程(在第11章将讨论),我们发现房间的平均吸声系数从0.08增加到0.15,吸声单位从48增加到89个沙宾。这种额外的吸声是由于与声音的衍射有关的边缘效应,使得给定的样本在声学上显得更大。换句话说,在这个例子中,65平方英尺的吸声材料的吸声效率只有四个16平方英尺的分布在房间中的材料的一半,四块材料的边缘总和大约是单个65平方英尺材料的两倍。因此,在房间内分布吸声材料的一个优点是其吸声效率大大增加,至少在某些频率下是如此。前面的陈述对于2千赫兹是正确的,但在700赫兹和8千赫兹时,单块和四块分布的材料之间的差异很小。
分布吸声材料的另一个重要结果是它有助于声音的扩散。吸声区块之间显示出反射表面的效果会改变波前,从而改善扩散效果。例如,将吸声模块沿着一面墙放置,可以分布吸收材料并改善效果,同时有助于声音的扩散。
凹面
凹面,如图9-6A所示,倾向于聚焦声能,因此应该避免使用,因为聚焦与我们通常寻求的扩散相反。曲率半径决定了聚焦的距离;凹面越平坦,声音聚焦的距离越大。这种表面经常导致麦克风放置时的问题。凹面可能在一个传声画廊中产生一些令人敬畏的效果,但在听音室和小型录音棚中应避免使用。
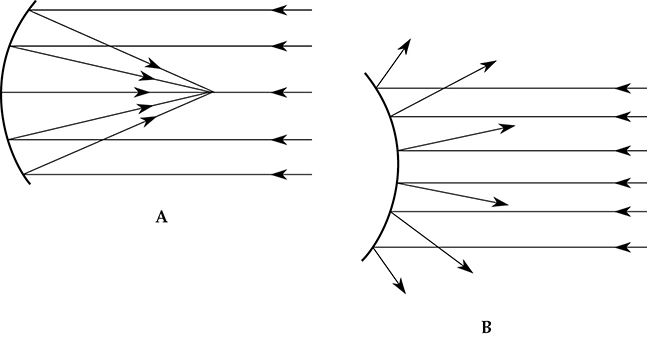
FIGURE 9-6 通常,凹面是不可取的,而凸面是非常理想的。(A)凹面倾向于聚焦声音。如果目标是实现良好的扩散声音,则应避免凹面。(B)凸面倾向于扩散声音。
凸面:多圆柱扩散器
多圆柱扩散器(简称“poly”)是一种有效的扩散元件,而且相对容易制造;它呈现出凸面的圆柱体截面。声音在这样的圆柱面上(由薄木板或硬纸板制成)时可能会发生三种情况:声音可以反射并因此分散,如图9-6B所示;声音可以被吸收;或者声音可以被再辐射。这样的圆柱元件在低频范围内作为吸收体发挥作用,因为在小房间中通常需要吸收和扩散。由于薄膜作用,再辐射的部分几乎均匀地辐射在大约120°的角度范围内,如图9-7A所示。类似的平面元件在辐射声音时的角度要窄得多,约为20°,如图9-7B所示。因此,反射、吸收和再辐射特性都倾向于使用圆柱面。在第12章中介绍了一些实用的多圆柱扩散器及其吸收特性。这些扩散器的尺寸并不是很关键,但要有效,它们的尺寸必须与所考虑的声音的波长相当。1000赫兹的声音波长略大于1英尺,而100赫兹的声音波长约为11英尺。一个3或4英尺的多圆柱体在1000赫兹处是有效的,但在100赫兹处则效果较差。总的来说,2到6英尺的多圆柱体底边或弦长和6到18英寸的深度基本上能满足大多数需求。在不同房间表面上的多个对称轴应该相互垂直。
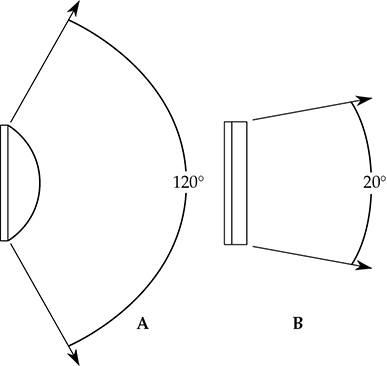
FIGURE 9-7 当适当设计时,多圆柱扩散器非常有效,可以提供宽带扩散。(A)多圆柱扩散器再辐射未被吸收的声能,辐射角度约为120°。(B)类似的平面元件辐射声音的角度要窄得多,约为20°。
重要的是,扩散元素应具有随机性。一面用多圆柱体衬砌的墙可能很美观,但对于扩散并不是非常有效。结构的规则性会导致其作为衍射光栅,影响某个特定频率的方式与其他频率大不相同,这与宽频扩散的理想相违背。
平面表面
由两个平面表面组成的几何声学扩散元件可形成三角形截面,由三个或四个平面表面组成的元件可形成多边形截面,也可以使用。一般来说,它们的扩散性能较圆柱截面差。
要点总结
• 在大多数房间设计中,扩散用于更有效地分布声音,并在整个房间提供更均衡的响应。
• 然而,过多的扩散可能会使声源的定位变得困难。
• 在实际房间中,声场与完全扩散差距很大;稳态响应可能显示出显著的频率和空间变化。
• 房间中的扩散程度可以通过低频混响衰减响应中的拍动信息来评估。
• 同样,非指数衰减的混响曲线表明真正的扩散条件并不存在。
• 混响时间的空间变化与房间中的扩散程度至少部分相关。
• 根据一项研究,几何扩散元件的深度至少必须是波长的七分之一才能产生效果。¹译注:指物理学家曼弗雷德·施罗德在贝尔实验室工作期间的研究。见这篇采访:https://www.aip.org/history-programs/niels-bohr-library/oral-histories/30536,不见于维基百科或教授的个人生平页面,也找不到相应论文。仅仅是一个工程上的近似公式。中文互联网常见的文章原文是这篇:https://www.subwoofer-builder.com/qrd.htm。
• 有反射墙面的吸音补丁在扩散声波前波面的改变上产生作用,从而改善了扩散效果。
• 多圆柱扩散器是一种有效的扩散元件,它呈现凸面的圆柱体截面,并提供反射、吸收和再辐射的有益特性。
• 为了提高效果,扩散元件应具有随机性。