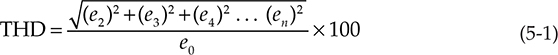《声学手册(第七版)》第五章
章节 5
信号、语音、音乐和噪声
语音、音乐和噪声等信号是大多数人都有共同经历的。拥有听力的我们对语音的声音非常熟悉;我们几乎每天都会听到语音。语音是人类交流的关键,而质量差的语音可极其令人沮丧。如果我们很幸运,每天还能听到音乐。音乐可以是最愉悦和最需要的人类体验之一。很难想象一个没有音乐的世界。噪声通常被认为是一种侵入性和不受欢迎的声音,常常混乱并干扰语音、音乐或沉默。本章探讨了语音、音乐和噪声之间的密切关系。
声音光谱仪
考虑到语音的声音,有必要了解这些声音是如何产生的。语音和音乐一样,具有高度的可变性和瞬态性,包括通过频率、声音水平和时间三维尺度移动的能量。声音光谱仪可以显示所有三个变量。每个声音都有其光谱特征,揭示了表征它的能量。几种常见的声音的光谱图显示在图5-1中。在这些光谱图中,时间从左到右水平推进,频率从原点向上增加,声音水平大致由迹线的密度表示——迹线越暗,该频率和该时刻的声音就越强烈。在这样的图上随着时间的推移,随机噪声显示为灰色、略带斑点的矩形,因为所有听觉范围内的频率和所有强度都随着时间的推移而表示。军鼓在某些点上接近随机噪声,但是它是间歇性的。狼哨以一个上升的音符开头,后面跟着一个间隔,然后是一个类似上升的音符,然后频率下降。警笛是一个音调,略带频率调制。
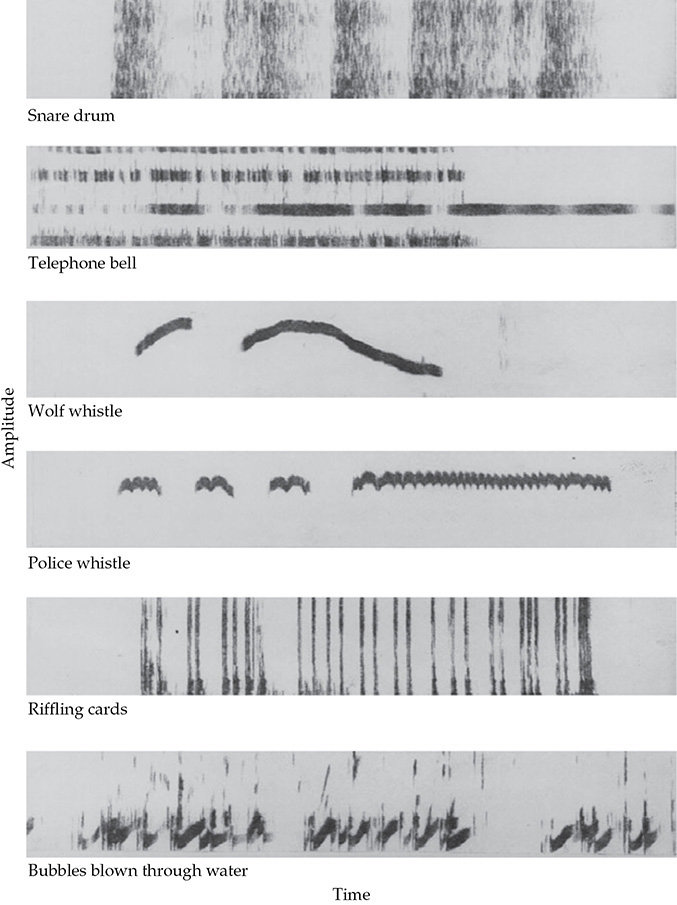
图5-1 常见声音的声谱图。时间向右推移,垂直轴表示频率,组成部分的强度由轨迹的强度表示。(AT&T贝尔实验室。)
人类的声音机制能够产生除了语音之外的许多声音。 图5-2 显示了一些这些声音的声谱图。在声谱图上,谐波序列以更或少垂直间隔的水平线条形式呈现在频率上。这些特点尤其在训练有素的女高音声音和婴儿的哭声中明显,但在其他声谱图中也可以看到痕迹。
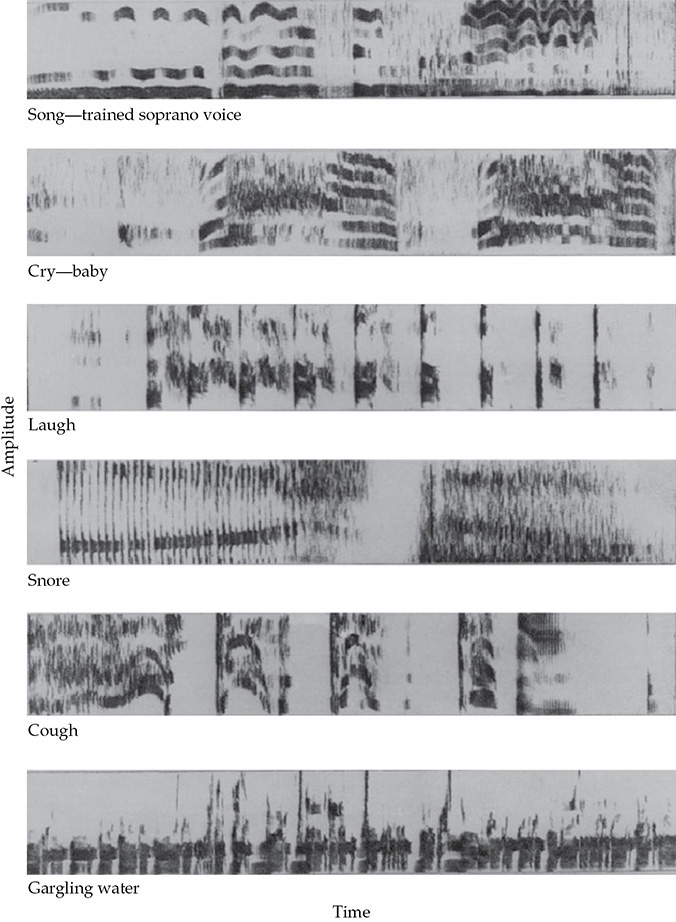
图5-2 除了语音之外的人类声音的声谱图。(AT&T贝尔实验室。)
语音
语音声音的产生包含两个准独立的组成部分:声源和声音系统。一般而言,语音是一个两阶段的过程,如图5-3A所示,原始声音由声源产生,然后在声道中进行形成。更准确地说,声音的三种不同来源由声音道塑造,如图5-3B所示。首先,我们自然想到的是声带发出的声音。这些声音形成了浊音。它们是由肺部流经开放声道、经过声带间的裂缝(声门)而导致声带振动的空气产生的。这一气流被分为气流脉冲,产生的声音几乎可以被称为周期性的,即一个周期跟随另一个周期。结果形成了元音音素,例如a、e、i、o和u。
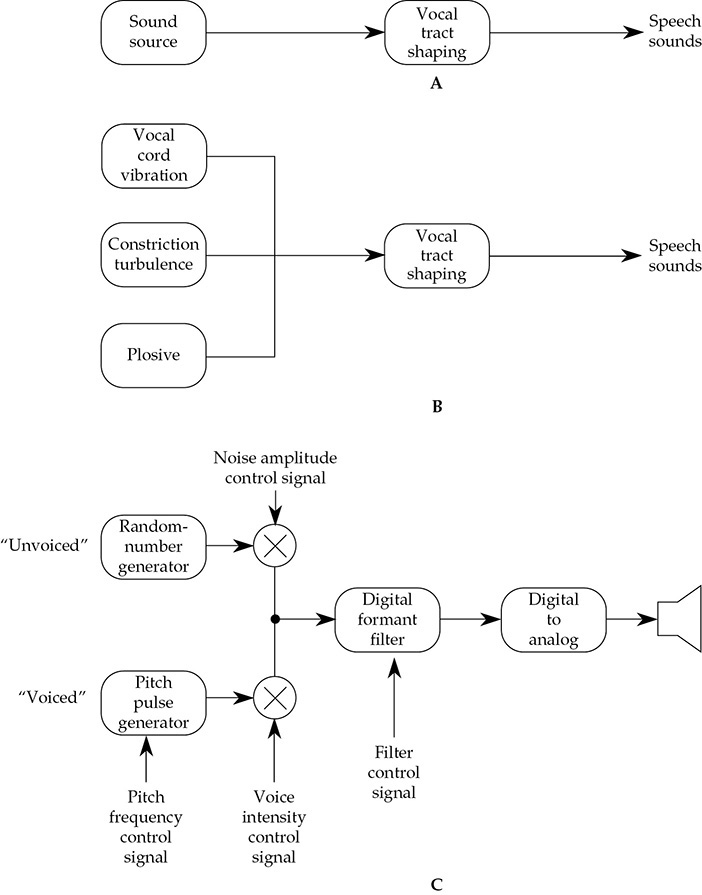
图5-3 人类语音的三个模型。(A)人类声音通过两个基本独立的组成部分相互作用产生:声源和声道的时变滤波作用。(B)声源由声带振动产生浊音、由气流湍流引起的摩擦音和破裂音组成。(C)用于合成人类语音的数字系统。
语音声音的第二个来源是通过在声道中的某一点通过牙齿、舌头或唇形成狭窄,并在足够高的压力下将空气强迫通过,产生明显的湍流。湍流空气产生噪声。这种噪声经过声道的塑造,形成语音中的摩擦音,如辅音f、s、v和z。试着发出这些声音,你会发现高速气流的参与程度很高。
语音声音的第三个来源是通过完全阻止呼吸,通常在口腔前部,建立压力,然后突然释放呼吸。试着发出辅音k、p和t,你会感受到这种破裂音的力量。它们通常会紧接着爆发出摩擦音或湍流声。这三种类型的声音——浊音、摩擦音和破裂音——是被塑造成我们所说的词语的原始来源。
声音源和信号处理可以在数字硬件或软件中实现。一个简单的语音合成系统如图5-3C所示。一个随机数生成器产生数字等效的无声组分的s声音。一个计数器产生模拟声带声音脉冲的脉冲信号,用于有声组分。这些信号通过时变数字滤波器进行塑形,模拟声道的变化共振。这些信号控制着每个组分,形成数字化的语音,然后转换为模拟形式。
语音的声道塑造
声道可以被视为一个声学共振系统。从声带到唇部的声道长度约为6.7英寸(17厘米)。它的横截面积由唇部、下颌、舌头和腭(一种可以打开或关闭鼻腔的门板)的位置决定,从0到约3平方英寸(20平方厘米)不等。鼻腔的长度约为4.7英寸(12厘米),体积约为3.7立方英寸(60立方厘米)。这些尺寸有助于确定声道的共振以及对语音声音的影响。
有声音的形成
如果将图5-3中的组成部分详细展开成声源频谱和调制函数,我们就会得到在音频中非常重要的一点,即声音中能量的频谱分布。我们还能更好地理解声音中有助于在混响和噪声存在下的语音可懂度的方面。 图5-4显示了产生有声音的步骤。首先,声音是由声带的振动产生的;这些声音是具有细致频谱的声脉冲,随着频率增加,其衰减率约为10 dB/八度,如图5-4A所示。声带的声音通过声道,它起到了一个时变滤波器的作用。 图5-4B中的峰值是由声道的声学共振,称为共振峰,产生的,声道起到了一个在声带端基本关闭且在口腔端开放的管道的作用。这样一个长度为6.7英寸的声学管道在奇数四分之一波长处共振;这些峰值出现在大约500、1,500和2,500 Hz左右。通过声道的共振形成的输出声音如图5-4C所示。这个分析适用于语音中的有声音。
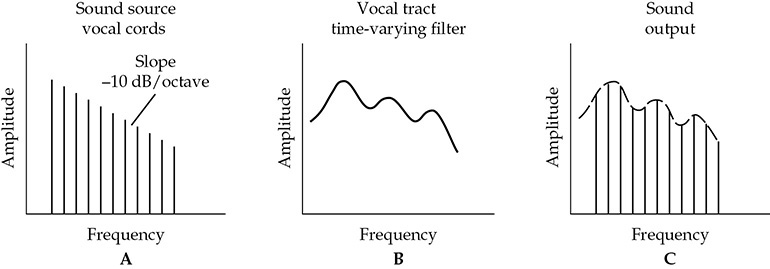
图5-4 有声音的产生可以看作是几个步骤。(A)声音首先由声带的振动产生;这些是具有频谱衰减的声脉冲。(B)声带的声音通过声道,起到时变滤波器的作用。声道的共振,称为共振峰,是声道的特点。(C)语音的有声音通过声道的共振形成。
无声音的形成
无声音的形成如图5-5所示。它们的产生方式与有声音的方式类似。无声音始于湍流空气产生的分布式、类似随机噪声的频谱,这些是摩擦音产生的。 图5-5A中的分布频谱是在声道的口腔端产生的,而不是声带端;因此,图5-5B的共振峰形状略有不同。 图5-5C显示了通过图5-5B的时变滤波器作用形成的声音输出。
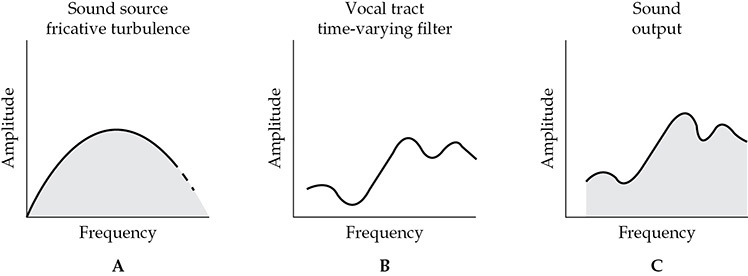
图5-5 描述摩擦音(如f、s、v和z)无声音产生的图示。 (A)由于声道狭窄而产生的气流湍流所致的分布频谱噪声。(B)声道的时变滤波器作用。(C)通过(A)的分布声音的滤波器作用产生的输出声音。
语音的频率响应
有声音由声带振动产生,无声音由湍流产生,爆破音则在唇附近产生,它们共同形成了我们的语音音素。当我们说话时,随着唇、颚、舌头和腭的位置改变以生成所需的单词,共振峰的频率也会发生变化。这就是人类语音在图5-6的频谱图中呈现出的复杂性。通过语音传达的信息是一种随时间迅速变化的频率和强度模式。请注意,在图5-6中,4 kHz以上的语音能量很少。尽管频谱图上没有显示,但100 Hz以下的语音能量也相对较少。因此,在2 kHz至3 kHz的区域存在频率峰值的原因是可以理解的,因为人类语音在这个范围内共振。
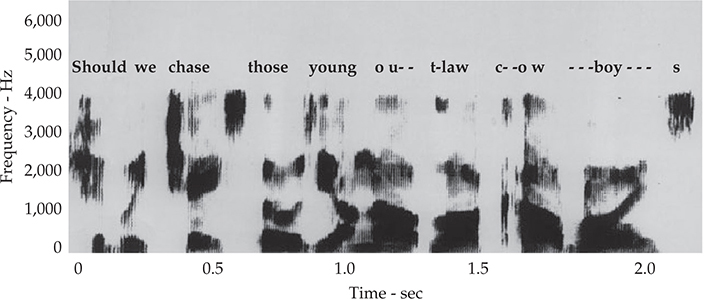
图5-6 男性声音说的一句话的声谱图。 (AT&T贝尔实验室)
语音的方向性
语音在各个方向上的音量级不同。这主要是由于口腔的方向性以及头部和躯干产生的声音阴影。 图5-7显示了语音方向性的两种测量结果。由于语音声音具有变化和复杂性,需要进行平均以获得准确的方向效应测量。
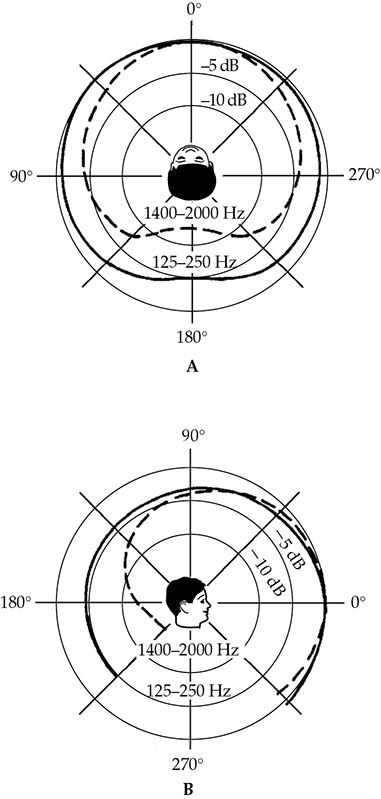
图5-7 人声具有方向性。 (A)关键语音频率的前后方向效应约为12 dB。(B)在垂直平面上,1,400 Hz至2,000 Hz频带的前后方向效应与水平平面上的效应大致相同。 (Kuttruff)。
在图5-7A中显示的水平方向效应只显示了125 Hz至250 Hz频带约5 dB的有限方向效应。这是可以预期的,因为与该频率带相关的波长为4.5到9英尺,而头部相对较小。然而,在1,400 Hz至2,000 Hz频带中存在明显的方向效应。对于这个包含重要语音频率的频带,前后方向差异约为12 dB。
在图5-7B中显示的垂直平面上,125 Hz至250 Hz频带的前后方向差异再次约为5 dB。对于1,400 Hz至2,000 Hz频带,前后方向差异与水平平面上的差异大致相同,除了躯干效应。很明显,拾音器接收高频语音频率的能力较差(参见图5-7B),尽管测量结果没有涵盖接近270°的角度。
音乐
音乐声音的复杂性非常多样。音乐声音可以从单一乐器或声音的近似正弦波简单性,到交响乐团的高度复杂的音调,其中每个乐器在每个音符上具有不同的音调质地。
弦乐器
小提琴、中提琴、大提琴、低音提琴或吉他等乐器通过弦的振动产生音调。在拉伸的弦上,泛音是基频(最低音)的确切倍数。因此,这些泛音可以适当地称为谐波。如果在弦的中间用弓弹奏,奇数谐波会得到强调,因为基频和奇数谐波在那里具有最大的振幅。由于偶数谐波在弦的中央处有节点,如果在那里用弓弹奏,偶数谐波会减弱。通常用弓弹奏的位置是靠近弦的一端,这样可以更好地融合偶数谐波和奇数谐波。在大多数音乐中,“不和谐的”第七谐波是不被接受的(在音乐上,它是一个非常平的小七度)。通过在距离一端的1/7或2/7处弓弹(或敲击或拨弦),可以减小这个谐波。因此,钢琴的锤子靠近第七谐波的节点。
小提琴的E音和G音的谐波内容显示在图5-8中。较高的E音的谐波倍数间距较宽,因此具有较薄的音色。另一方面,较低的G音具有间距较小的频谱分布和更丰富的音色。小提琴相对于低频的G弦的小尺寸意味着共鸣的琴身无法产生与较高的谐波一样高强度的基频。谐波内容和频谱形状取决于共鸣的小提琴琴身的形状和大小,木材的类型和状态,甚至是清漆。为什么在众多的优秀小提琴中,真正杰出的小提琴如此少,这是一个尚未完全解答的问题。
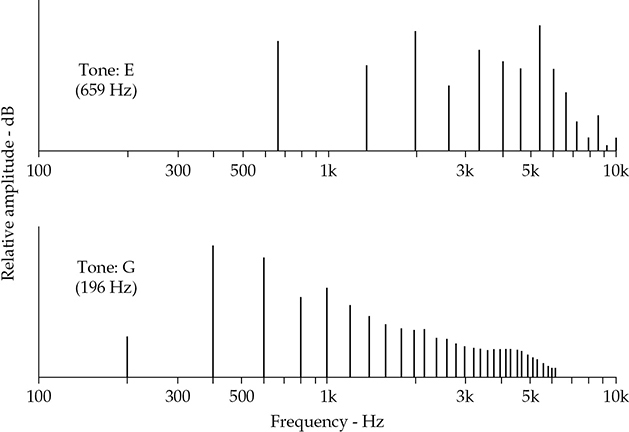
图5-8 显示小提琴开放弦的谐波内容的频谱图。由于谐波密集排列,低频音调听起来更丰富。
吹奏乐器
在许多乐器中,管道或管的共鸣主要可以看作是一维的。(三维空间中的共鸣将在后面的章节中讨论。)在管道中,驻波效应是主导因素。如果空气被封闭在一根两端都封闭的窄管中,将会产生基频(管的长度的两倍)和其所有谐波。在只有一端开口的管中,共振将在管长为波长的四倍时发生,并产生奇数谐波。吹奏乐器就是以这种方式形成声音的;气柱的长度可以连续变化,如滑音长号,或跳跃变化,如小号或法国号,或通过在气柱长度上开启或关闭孔来实现,如萨克斯管、长笛、单簧管和双簧管。
各种吹奏乐器的谐波内容与小提琴的对比显示在图5-9的频谱图中。每种乐器都有其特有的音色,由其谐波的数量和强度以及乐器的结构共振对谐波列的共振形状所决定。
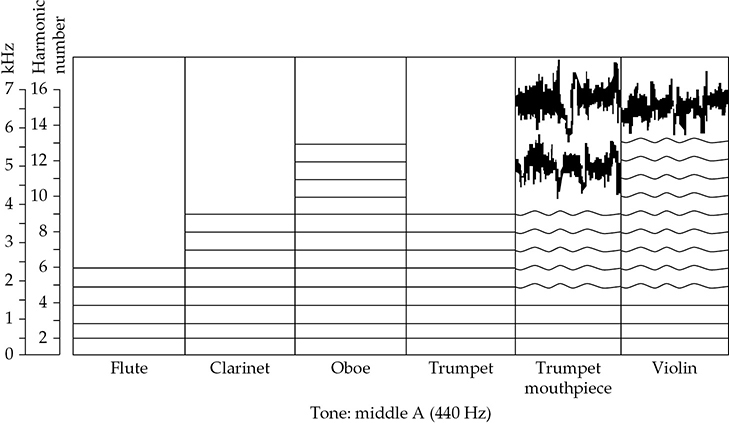
图5-9 显示各种木管乐器和小提琴演奏中音高A(440 Hz)的谐波内容的频谱图。显示的差异解释了不同乐器的音色差异。(AT&T贝尔实验室)
非谐波泛音
一些乐器产生一种复杂的非谐波泛音。鼓的泛音不是谐波相关的,尽管它们为鼓的声音增添了丰富性。三角铁、钟和铙钹产生的泛音混合物与其他乐器相当融合。钢琴弦是坚硬的弦,其振动方式类似于实心杆和拉伸弦的组合。因此,钢琴的泛音不是严格的谐波。非谐波泛音负责产生风琴和钢琴声音之间的差异,并为音乐声音带来了多样性。
语音和音乐的动态范围
语音的动态范围相对有限。从最轻柔的声音到最响亮的语音声音,以正常力度说话的声音可能具有30到40 dB的动态范围。用更大的力度,响亮语音的范围可能为60到70 dB。即使这个范围也可以很容易地适应音频录制技术。然而,对于录制和传输音乐来说,历史上一直是一个更具挑战性的问题。
在音乐厅中,一个完整的交响乐团能够产生非常响亮的声音,但也有柔和、细腻的乐段。作为观众坐在观众席上,我们可以充分感受到由于人耳的极大动态范围而产生的声音扫描。最响亮的乐段与最柔和的乐段之间的动态范围可能达到100 dB(人耳的动态范围约为120 dB)。为了有效果,柔和的乐段仍然必须在音乐厅中的环境背景噪声之上能够听到,因此要重视足够的声学隔离以防止交通和其他外部噪声的干扰,并采取措施确保空调设备的噪声低。
对于那些无法亲临音乐厅的人来说,现场广播、电视广播或录音可能就是唯一的选择。传统的模拟广播,例如模拟调频(FM)传输,无法处理整个交响乐团的完整动态范围。低频极端的噪音和高频极端的失真引入了限制。此外,广播监管限制禁止对相邻信道的干扰,这也限制了动态范围。
理想情况下,数字音频具有完全捕捉音乐所需的动态范围和信噪比。数字系统中的动态范围与二进制数字(比特)的字长直接相关,如表5-1所示。例如,一张CD存储16位字,因此可以存储具有96 dB动态范围的音乐;如果信号经过适当抖动处理,这个范围可以扩展。消费者格式,如蓝光音频光盘以及专业音频录音机,可以提供24位分辨率,并避免由后续信号处理引起的数字伪像的可听性。当充分利用技术的优势时,数字技术主要将动态范围限制从录音介质转移到播放环境。另一方面,如AAC、MP3和WMA等数字格式提供的动态范围和保真度可能相当不稳定;它们的质量取决于记录或流式传输文件的比特率等因素。
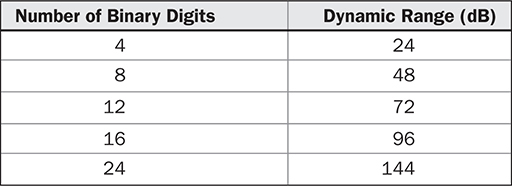
TABLE 5-1 数字字长的理论动态范围
语音和音乐的功率
在许多应用中,必须考虑声源的功率。对于会话语音,平均功率可能为20 μW,但峰值功率可能达到200 μW。大部分语音的功率集中在中低频段,80%的功率位于500 Hz以下,但在100 Hz以下的功率非常小。另一方面,高频段上的少量功率是辅音所在的地方,决定了语音的可懂性。在这个范围之外的更高频率和更低频率为语音增添了自然的特质,但对可懂性没有贡献。
乐器可以产生比人声更高的功率。例如,长号可能产生6 W的峰值功率,一个完整的交响乐团的峰值功率可能为70 W。各种音乐乐器的峰值功率水平列在表5-2中。
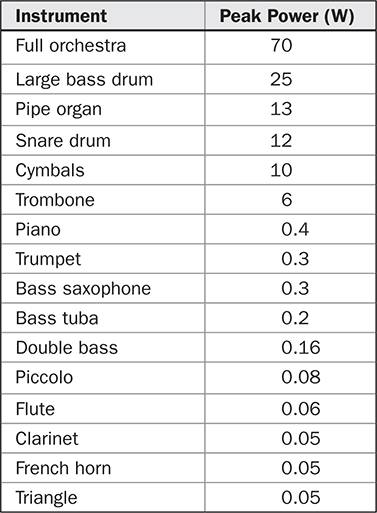
TABLE 5-2 音乐声源的峰值功率(Sivian et al.)
语音和音乐的频率范围
比较各种乐器和语音的频率范围是很有教育意义的。这最好通过图形来完成。图5-10显示了各种乐器和人声的范围。需要注意的是,这个图只显示了基频音高,而没有显示谐波泛音。非常低的风琴音符主要通过其谐波来感知。某些伴随乐器的高频噪音没有包括在内,例如木管乐器的簧片噪音、弦乐器的弓弦噪音,以及钢琴和打击乐器的按键咔嗒声和敲击声。
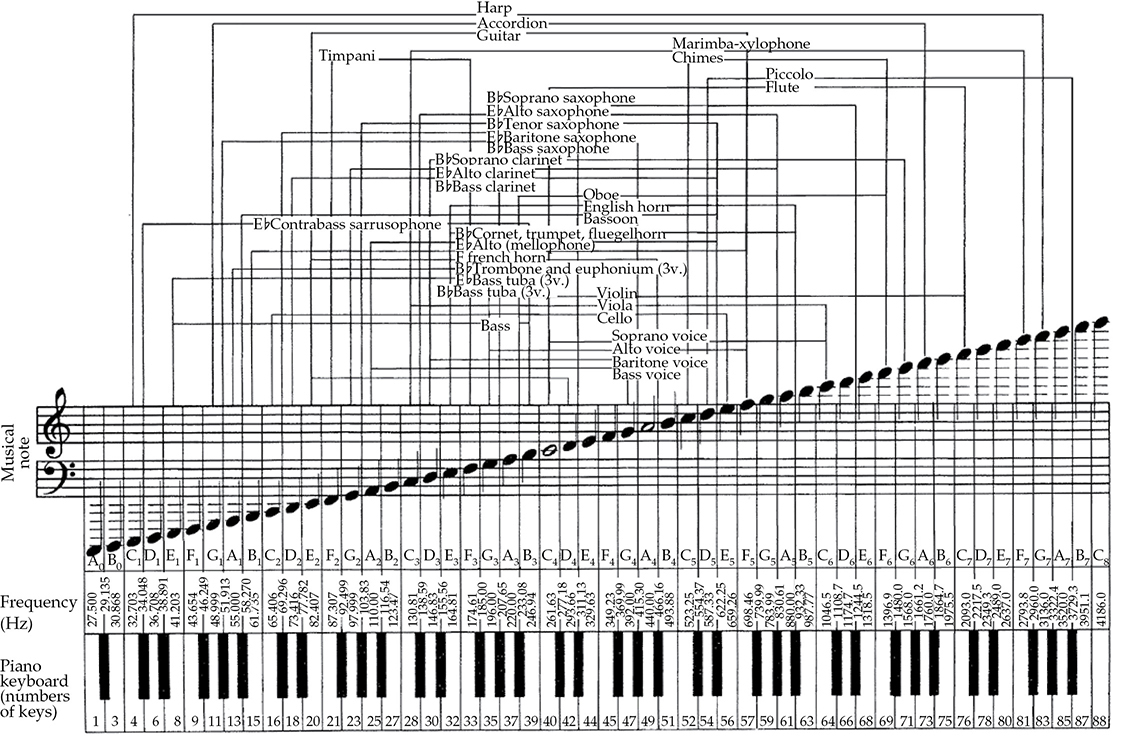
FIGURE 5-10 各种乐器和人声的可听频率范围。只包括基音;偏差音(未显示)的频率更高。也未显示许多产生的高频附带噪音。(C. G. Conn,有限公司。)
语音和音乐的听觉范围
语音、音乐和其他声音的频率范围和动态范围对人耳提出了不同的要求。语音只使用了耳朵听觉能力的一小部分。语音所使用的听觉区域在图5-11中的阴影区域显示。这个区域位于听觉范围的中央部分;普通语音中不存在极为柔和或极为响亮的声音,也没有非常低频或非常高频的声音。在图5-11中表示的语音区域是从长时间平均值中得出的,理想情况下,它的边界应该用渐变表示,以表示水平和频率的瞬时变化。所表示的语音区域平均动态范围约为42 dB。170 Hz至4,000 Hz的频率范围涵盖了大约4.5个八度。
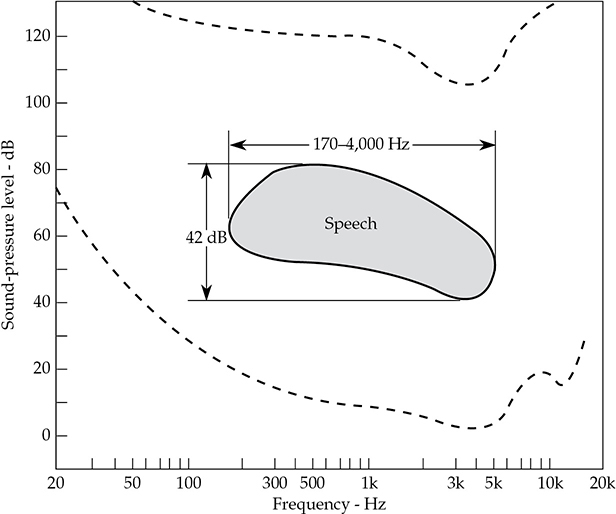
FIGURE 5-11 用于语音声音的听觉区域部分。
在图5-12中显示的音乐区域比图5-11中的语音区域要大得多。音乐使用了耳朵听觉范围的较大部分。与语音相比,它在水平和频率上的波动相应更大。同样,长时间平均值用于确定音乐区域的边界,边界应该使用渐变来考虑极值。所示的音乐区域非常保守;它的动态范围约为75 dB,频率范围约为50 Hz至8,500 Hz。这个频率跨度约为7.5个八度,而人耳的范围为10个八度。高保真的标准要求比这个更宽的频率范围。在确定语音和音乐区域时涉及到的平均过程之外,动态范围和频率范围将更大,以适应对整体平均值贡献很小但仍然非常重要的短期瞬变。
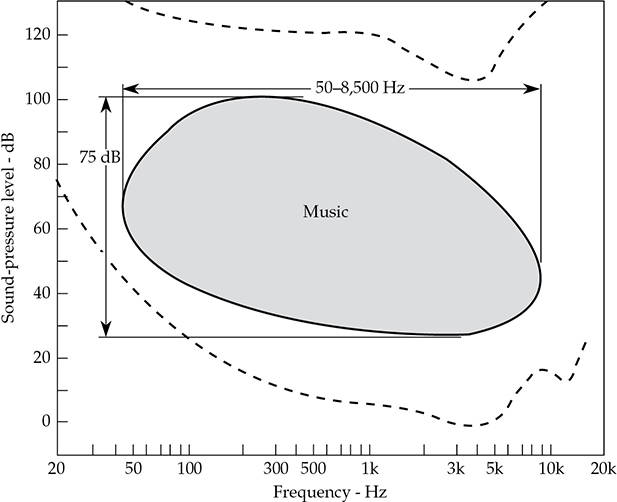
FIGURE 5-12 用于音乐声音的听觉区域部分。
噪声
“信号”一词意味着正在传递信息。噪声也可以被视为一种信息传递载体。例如,通过打断噪声形成点和划线是将噪声转化为通信的一种方式。我们还将看到,衰减的一段噪声可以提供有关房间声学质量的信息。另一方面,有许多类型的噪声是不受欢迎的,比如响铃的手机和繁忙的交通声。有时很难区分令人反感的噪声和合法的信息传递载体。例如,汽车的噪声传达了关于其运行状况的大量信息。音频播放系统可以产生业主认为非常理想的声音,但对邻居来说可能被认为是侵入性的。大声的救护车或消防车警报器被专门设计为既令人反感又传达重要警报。社会建立了限制,以使令人反感的噪声最小化,同时确保需要听到它们的人能够听到携带信息的声音。
我们对噪声的评估很大程度上是主观的反应。通常,高频噪声比低频噪声更令人讨厌。间断性噪声比稳定或持续的噪声更令人讨厌。移动和非定位的噪声比固定和定位的噪声更令人讨厌。无论如何评估,噪声干扰可能是轻微的困扰,或者可能导致严重的后果,如听力损伤。
噪声测量
将噪声定义为不需要的声音适用于许多种类的噪声,但噪声也是声学测量中的重要工具。这种噪声不一定与不需要的噪声不同,只是将噪声用于有益的用途。
在声学测量中,纯音通常很难使用,而以同一频率为中心的一段窄带噪声可以进行令人满意的测量。例如,一个从扬声器接收1 kHz纯音信号的录音棚麦克风的输出在不同位置上会因房间谐振而有很大变化。然而,如果从相同的扬声器辐射出以1 kHz为中心的一个频宽为一个八度的噪声带,从位置到位置的级别趋于更加均匀,同时测量中会包含有关1 kHz区域发生的情况的信息。这样的测量技术是有意义的,因为我们通常对录音棚或听音室如何对待正在录制或重现的复杂声音感兴趣,而不是对稳定的纯音感兴趣。
随机噪声
随机噪声在任何模拟电路中都会产生,并且减小其影响通常是一个困难的问题。如图5-13所示,正弦波和随机噪声信号在示波器上的显示形式截然不同。其中一个的规律性与另一个的随机性形成鲜明对比。如果示波器的水平扫描足够扩展,并且捕获随机噪声信号的一部分,结果将如图5-14所示。
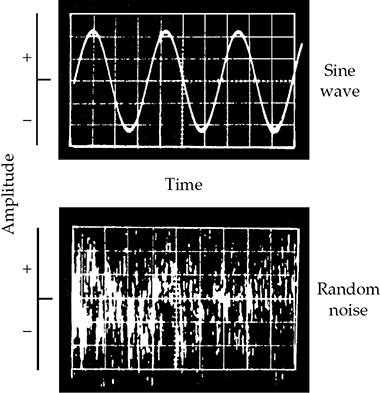
FIGURE 5-13 正弦波和随机噪声的示波图。随机噪声在振幅、相位和频率上不断变化。
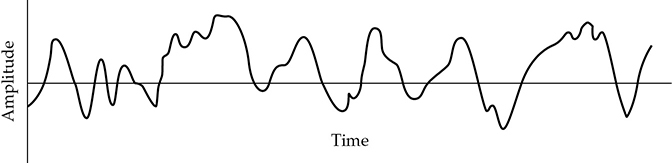
FIGURE 5-14 图5-13中的随机噪声信号的一部分在时间上展开。噪声信号的非周期性特性显而易见;波动是随机的。
如果噪声具有幅度呈正态或高斯分布,那么它被认为是纯随机的。这意味着如果我们在许多等间隔的时间点对瞬时电压进行采样,一些读数将是正数,一些是负数,一些较大,一些较小,并且这些样本的绘图会逼近图5-15所示的熟悉的高斯分布曲线。
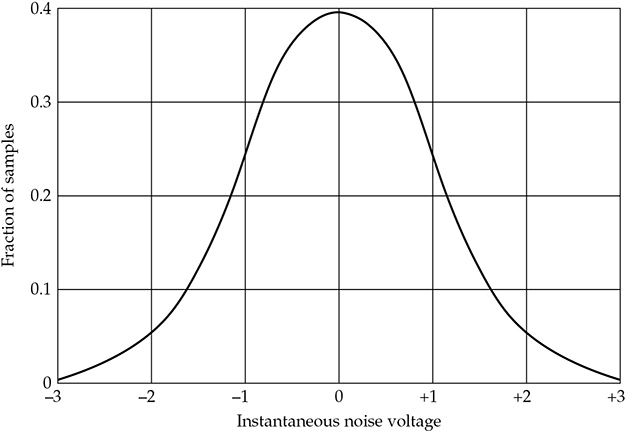
FIGURE 5-15 证明噪声信号的随机性在于对瞬时电压进行采样,例如在时间上等间隔的1,000个点上,并绘制结果。如果噪声是随机的,就会得到熟悉的钟形高斯分布曲线。
白噪声和粉噪声
白噪声和粉噪声经常用作测试信号。白噪声类似于白光,因为它们的能量在整个频谱中均匀分布。换句话说,白噪声在每个1 Hz频带中具有相同的平均功率。有时候会说白噪声在每赫兹上有相等的能量。因此,当在对数频率刻度上绘制白噪声时,它会展现出能量随频率均匀分布的特点,如图5-16A所示。由于每个较高的八度包含的1 Hz频带是前一个八度的两倍,白噪声的能量在每个较高的八度中翻倍。因此,白噪声听起来像是高频的嘶嘶声。
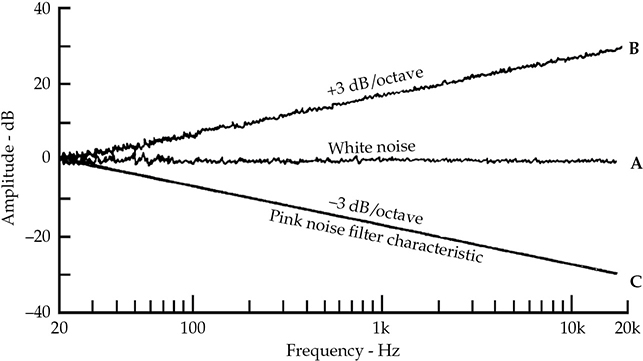
FIGURE 5-16 噪声信号的频谱。(A)随机白噪声具有每赫兹恒定的能量。如果使用固定带宽的分析仪测量随机白噪声的频谱,结果将呈现出与频率平坦的特性。(B)如果使用带通宽度为其调谐频率的一定百分比的分析仪测量白噪声,频谱将以每八度3 dB的斜率上升。(C)粉噪声是通过对具有每八度下降3 dB的特性的白噪声进行低通滤波获得的。
白光经过棱镜分解成一系列颜色。红色与较长的光波长相关,即较低频率的光。粉噪声在每个八度(或1/3八度)频带中具有相同的平均功率。由于连续的八度包含逐渐增大的频率范围,粉噪声在低频上具有相对较高的能量。因此,粉噪声在低频上具有更显著的声音,而不同于白噪声。粉噪声被具体定义为在低频区域具有特定下降斜率(-3 dB/八度)的噪声,如图5-16C所示。一般而言,粉噪声常用于声学测量,而白噪声则用于电学测量。这是因为粉噪声的能量分布更接近人耳主观听觉的方式。使用粉噪声时,如果使用常数百分比带宽的滤波器(如八度或1/3八度滤波器),则会得到平坦的响应。在测量系统时,将粉噪声应用于输入端,如果系统是平坦的,输出响应(例如使用1/3八度滤波器)也将是平坦的。
这些白噪声和粉噪声的术语的起源是因为使用了两种类型的频谱分析仪。一种是恒定带宽分析仪,它在通过频谱时具有固定宽度的通带。例如,可以使用5 Hz的带宽。如果使用恒定带宽分析仪测量具有平坦频谱的白噪声,由于固定带宽会在整个频带测量出恒定的能量(参见图5-16A),所以会得到另一个平坦的频谱。
相比之下,在恒定百分比带宽分析仪中,带宽会随频率变化。其中一种常见的类型是1/3八度分析仪,其带宽在整个可听频率范围内与人耳的关键带宽相对较为匹配。在100 Hz时,1/3八度分析仪的带宽为23 Hz,而在10 kHz时,带宽为2,300 Hz。显然,在以10 kHz为中心的1/3八度频带
上,它截取到的噪声能量要比以100 Hz为中心的频带更大。使用恒定百分比带宽分析仪测量白噪声将得到一个斜率为+3 dB/八度的向上倾斜的结果(参见图5-16B)。
在许多音频频率的测量中,仪器和房间的理想特性是在整个频率范围内具有平坦响应。假设要测量的系统的频率特性几乎是平坦的。如果使用白噪声驱动该系统,并使用恒定百分比带宽分析仪进行测量,结果将具有+3 dB/八度的向上倾斜。如果测量结果在名义上是平坦的,那么与平坦度的偏离将非常明显。通过将白噪声通过低通滤波器(例如图5-17所示的滤波器),可以获得一个具有向下斜率(-3 dB/八度)的接近平坦的噪声。使用这种粉噪声驱动的接近平坦的系统(如放大器或房间)将产生接近平坦的响应,从而使得与平坦度的偏离非常明显。
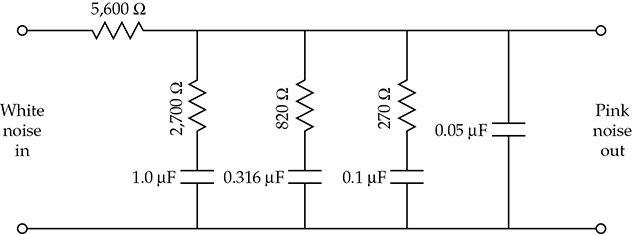
FIGURE 5-17 用于将白噪声转换为粉噪声的简单滤波器。它将每赫兹具有恒定能量的白噪声转换为每八度具有恒定能量的粉噪声。粉噪声在使用通过带宽与中心频率的百分比恒定的分析仪进行声学测量时最有用。
信号失真
在讨论音频信号时,我们不能忽视信号在经过换能器、放大器和各种形式的信号处理设备时可能发生的情况。以下是一些可能的失真形式:
• 带宽限制 如果放大器的通带削弱低频或高频,输出信号与输入信号之间的差异就是这个带宽的减小。
• 非均匀响应 通带内的峰谷会改变信号的波形。
• 相位失真 引入的相移会影响信号组成部分之间的时间关系。
• 动态失真 压缩器或扩展器改变了信号的原始动态范围。
• 交叉失真 在B类放大器中,输出器件只在一个周期的一半导通,靠近零输出的不连续性会导致交叉失真。
• 非线性失真 如果放大器是真正线性的,输入和输出之间存在一对一的关系。放大器反馈有助于控制非线性倾向。人耳不是线性的。当纯音传入耳朵时,会听到谐波。如果同时播放两个响亮的音调,耳朵本身会产生它们的和与差音,这些音调以及它们的谐波都可以听到。对放大器进行交调测试基本上是做同样的事情。如果放大器(或耳朵)完全线性,就不会产生和与差音或谐波。产生在输入信号中不存在的频率成分是非线性失真的结果。
• 瞬态失真 打击钟铃,它会响起。将瞬态波前信号应用于放大器,它的响应也可能会产生共鸣。因此,钢琴音符等信号很难再现。音调爆发测试信号分析设备的瞬态响应特性。瞬态互调失真、斜率诱导失真和其他测量技术评估瞬态形式的失真。
谐波失真
谐波失真方法是评估电路非线性效应的普遍方法。在这种方法中,测试设备被驱动以高纯度的正弦波。如果信号遇到任何非线性,输出波形将发生变化;也就是说,会出现不在纯正弦波中的谐波分量。对输出信号进行谱分析可以测量这些谐波失真成分。
例如,波形分析仪可以使用恒定的通带宽度为5 Hz,扫描音频频谱。图 5-18 显示了这样一次测量的结果。首先,将波形分析仪调至基波 f0 = 1 kHz,并将电平设置为方便的1.00 V。波形分析仪显示2f0 的第二次谐波在2 kHz处的幅度为0.10 V。3f0 的第三次谐波在3 kHz处的读数为0.30 V,第四次谐波的读数为0.05 V,依此类推。数据汇总在 表 5-3 中。
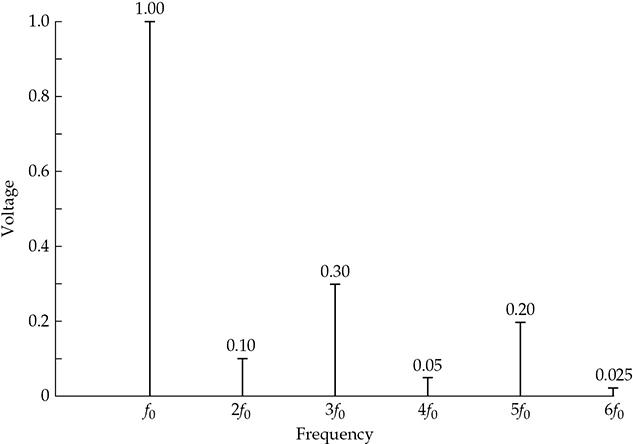
FIGURE 5-18 用恒定带宽分析仪测量失真周期波。基波 f0 被设定为某个参考电压,这里取1.00 V。使用波形分析仪,测量了2f0 处的第二次谐波幅度为0.10 V。波形分析仪同样给出了每个谐波的幅度。然后将谐波电压的均方根 (RMS) 与1.00 V 的基波进行比较,以得到以百分比表示的总谐波失真 (THD)。
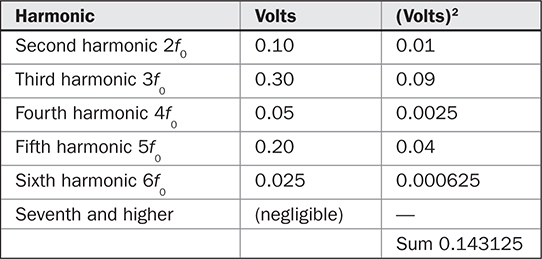
表 5-3 谐波失真产物(基波 f0 = 1 kHz,幅度为 1.00 V)
总谐波失真 (THD) 可以通过以下公式计算:
其中,e2、e3、e4,...,en = 第二、第三、第四等谐波的电压
e0 = 基波电压
在 表 5-3 中,谐波电压已经被平方并相加。使用以下方程式:

37.8% 的 THD 是一种非常高的失真程度,会使任何放大器在任何类型的信号下听起来都很差,但这个例子已经达到了我们的目的。
THD 方法还可以进行简单的改进。再次考虑 图 5-18。如果将 f0 基波调整到某个已知值,然后将陷波器调整到 f0 并基本上将其消除,只剩下谐波。使用均方根 (RMS) 仪器测量这些谐波,就可以完成公式 (5-1) 中的平方根部分。将测量得到的谐波分量的 RMS 值与基波的 RMS 值进行比较,并将其表示为百分比,即可得到 THD。
一个无失真的正弦波经过放大器,正峰被截断,如 图 5-19 所示。在左边,可以明显看到带有 5% THD 的正峰变平的情况,在下方显示了除去基波后所有谐波产物的综合总和。右边显示了更大的截断效果,产生 10% 的 THD。图 5-20 显示了一个正弦波通过放大器,并对正负峰进行对称截断的情况。对于对称截断产生的失真产物具有略微不同的外观,但测量得到的 THD 相同:5% 和 10%。
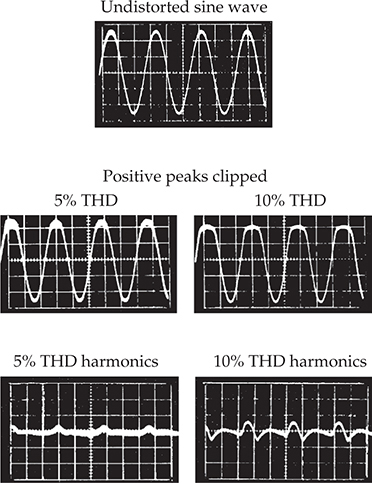
图 5-19 示波图显示了一个无失真的正弦波,该波形被应用于放大器的输入端,放大器对信号的正峰进行截断。展示了 5% 和 10% THD 的截断正弦波形状。如果基波被陷波器排除,合并的谐波将呈现如图所示的形态。
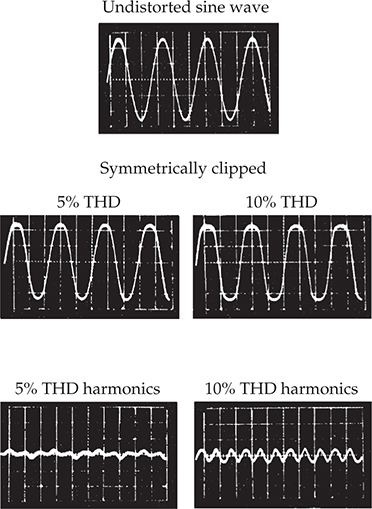
图 5-20 示波图显示了一个无失真的正弦波,该波形被应用于对称地截断正负峰的放大器的输入端。展示了 5% 和 10% THD 的截断正弦波形状。还展示了仅包含谐波的形态,基波被滤除。
消费级功放通常的规格列表上会显示 THD 接近 0.05%,而不是 5% 或 10%。在一系列双盲主观测试中,Clark 发现在不同类型的声音上可以听到 3% 的失真。对于精心选择的素材(如长笛独奏),可能能够检测到低至 1% 或 2% 的失真。对于正弦波,1% 的失真是可以听到的。
共振
任何共振系统的振动幅度在共振频率 f0 处最大,在低于和高于该频率的频率下幅度较小。在该共振频率上进行适度激励信号将导致较高的振幅。如 图 5-21 所示,随着激励频率的变化,振动幅度也会发生变化,在共振频率处经历峰值响应。也许最简单的共振系统示例是弹簧上的质量。
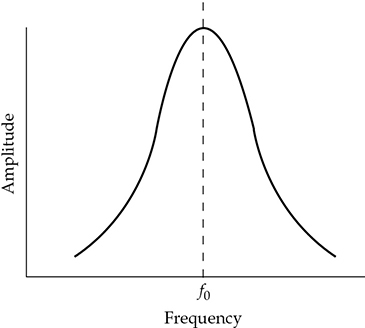
图 5-21 任何共振系统的振动幅度在自然或共振频率 f0 处最大,在低于和高于该频率的频率下减小。
这种共振效应在各种系统中都会出现:机械系统(如音叉)的质量和刚度的相互作用,或者瓶子中空气的声学共振,即瓶颈中的空气质量与瓶身中被困住的空气的弹性作用相互作用。共振在建筑声学中尤为重要。大多数房间可以被视为封闭空间;它们本质上是空气的容器。因此,它们表现出模态共振。正如我们将在后面的章节中看到的,共振频率是房间内部尺寸的函数。
在电子电路中,共振效应也存在,因为电感的惯性效应与电容的储能效应相互作用。电感器(其电气符号为 L)通常是一个线圈,而电容器(C)由导电材料的片层组成,这些片层由非导电材料隔开。能量可以储存在电感器的磁场中,也可以储存在电容器的电极上的电荷中。两个这样的储能系统之间的能量交换可以产生共振效应。
图 5-22 展示了两个电路,其中电感器和电容器可以表现出共振。假设在并联共振电路中有一个变化频率但振幅恒定的交流电流流动(参见 图 5-22A)。随着频率的变化,电压在端口处达到 LC 系统的自然频率时达到最大值,并在较低和较高频率下降。这样形成了典型的共振曲线形状。换句话说,并联共振电路在共振时表现出最大阻抗(阻碍电流流动)。
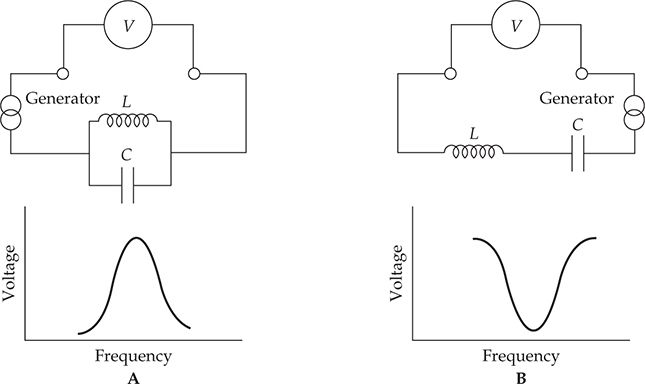
图 5-22 (A)并联共振和(B)串联共振的比较。对于流过的恒定交流电流,与并联共振电路相比,串联共振电路的电压达到最小值。
串联共振电路(参见 图 5-22B)也使用电感器 L 和电容器 C。当具有恒定幅度但变化频率的交流电流在电路中流动时,端口处的电压描述了一个倒置的共振曲线,其中电压在自然频率处达到最小值,并在较低和较高频率下升高。也可以说,串联共振电路在共振频率下呈现最小阻抗。
音频滤波器
滤波器在许多应用中使用,包括音频均衡器和扬声器分频器。在模拟滤波器设计中,通过选择电阻、电感和电容的值,可以获得几乎任何类型的频率和阻抗匹配特性。常见的滤波器包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。这些滤波器的特征频率响应如图 5-23 所示。图 5-24 显示了电感器和电容器可以如何在各种被动电路中排列,以形成简单的高通和低通滤波器。图 5-24C 中的滤波器的截止更加陡峭,比图 5-24A 和 B 中的简单滤波器更加陡峭。还有许多其他具有特定特性的高度专业化的滤波器。通过使用这些滤波器,可以随意改变宽带信号(如语音或音乐)。
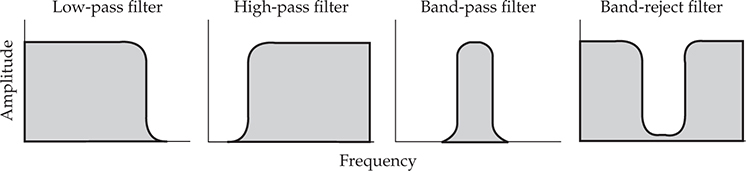
图 5-23 低通、高通、带通和带阻滤波器的频率响应特性。
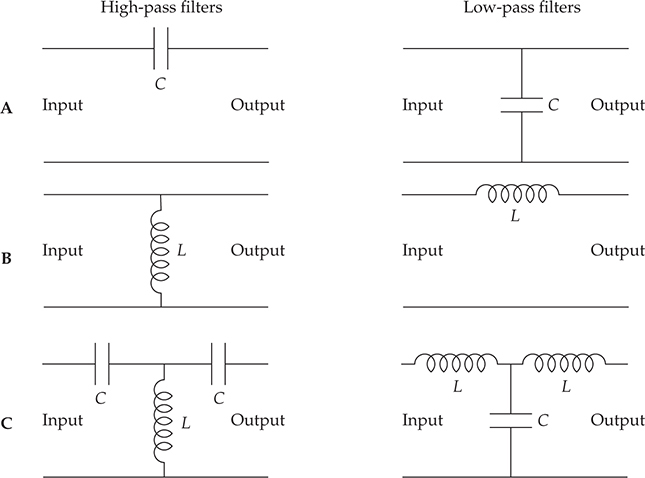
图 5-24 电感器和电容器可以用来组成被动高通和低通滤波器。 (A)使用电容器的滤波器。 (B)使用电感器的滤波器。 (C)同时使用电容器和电感器的滤波器;这些滤波器的截止频率比(A)或(B)中的滤波器更陡峭。
可调滤波器可以在其设计频段内移动到任何频率。一种类型是恒定带宽滤波器,在任何频率下提供相同的带宽。例如,频谱分析仪可能具有5 Hz的带宽,无论它调谐到100 Hz还是10 kHz,或者其操作频段内的任何其他频率。另一种可调滤波器提供的通过带宽是其调谐频率的一个恒定百分比。1/3倍频带滤波器就是这样一种设备。如果它调谐到125 Hz,那么1/3倍频带的带宽是112 Hz到141 Hz。如果它调谐到8 kHz,1/3倍频带的带宽是7,079 Hz到8,913 Hz。在任一情况下,带宽约为其调谐频率的23%。
被动滤波器不需要任何电源。主动滤波器依赖于有源电子设备,如离散晶体管或集成电路,来实现其功能。图 5-25A 显示了由电感器和电容器组成的被动低通滤波器。图 5-25B 显示了基于运放集成电路的主动低通滤波器。被动滤波器和主动滤波器都被广泛应用;根据应用的不同,它们都具有各自的优势。

图 5-25 显示了两个模拟低通滤波器。(A)被动模拟滤波器。(B)利用运放集成电路的主动模拟滤波器。
滤波器可以以模拟或数字形式构建。到目前为止,讨论的所有滤波器都属于模拟类型;它们对连续的模拟信号进行操作。数字滤波器对离散时间采样的数字音频信号执行数值运算。在许多情况下,数字滤波器以在微处理器上运行的软件程序的形式实现;模数转换器和数模转换器用于通过数字滤波器传输模拟音频信号。图 5-26 显示了一个数字滤波器的示例。这个示例是一个有限冲激响应(FIR)滤波器,有时也被称为横向滤波器。数字样本输入到滤波器,并应用于由带有延迟线的 z−1 块组成的顶部部分;中间部分显示了与滤波器系数的乘法;这些输出被求和以产生滤波器的输出样本。通过这种方式,信号的频率响应可以被改变。
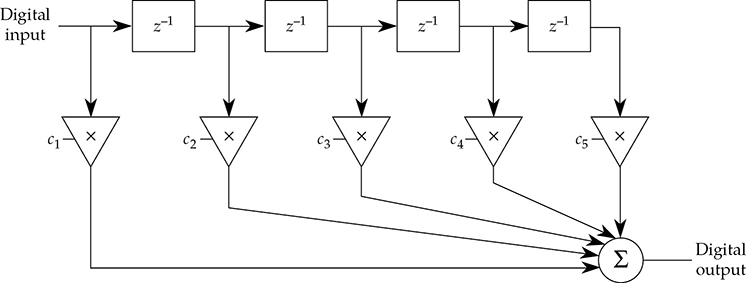
图 5-26 有限冲激响应(FIR)滤波器,显示延迟、乘法和求和以实现信号滤波。
数字滤波器是数字信号处理(DSP)技术的一部分。在音频行业中,DSP广泛应用于许多不同的应用,包括音乐信号处理和房间声学信号分析。例如,DSP可以应用于扬声器-房间-听者问题。放置在听音位置的麦克风测量了听音室中扬声器输出的频率和相位响应,然后可以根据这些数据创建反向均衡,以补偿由扬声器和房间声学引起的异常情况。
要点
• 语音和音乐一样,具有高度的变化性和瞬时性,包括能量在频率、声级和时间三个维度上的传递。
• 声道可以被视为一个声学共振系统。其尺寸有助于确定声道的共振以及其对语音音素的影响。
• 声音的频谱能量分布有助于确定语音的可懂性,相对于混响和噪声的频谱分布。
• 音乐声音的复杂性非常大,从接近正弦波的简单性到高度复杂的音调变化。音乐的动态范围可能达到100 dB(耳朵的动态范围约为120 dB)。
• 音乐乐器可以产生相对较高水平的声功率。例如,一个完整的交响乐团的峰值功率可能为70瓦。
• 许多噪声是不可取的,因此需要重视降低噪声水平;然而,噪声也是声学测量中的重要工具。在许多情况下,以某个频率为中心的窄带噪声被使用。
• 白噪声和粉红噪声通常被用作测试信号。白加权随机噪声在每个1 Hz频段中具有相同的平均功率。粉红加权随机噪声在每个八度(或1/3八度)频段中具有相同的平均功率。由于连续的八度包含越来越大的频率范围,粉红噪声在低频具有相对较多的能量。
• 任何共振系统的振动幅度在其固有或共振频率上最大,在该频率下方和上方的频率上较小。在该共振频率下的适度激励信号可以导致高振幅。
• 大多数房间可以被视为封闭空间;它们本质上是空气的容器。因此,它们具有模态共振。
• 滤波器在许多应用中使用,包括音频均衡器和扬声器分频器。常见的滤波器形式包括低通、高通、带通和带阻滤波器。