《声学手册(第七版)》第三章
章节 3
自由场中的声音
许多实际的声学问题与房间、建筑物以及汽车和飞机等车辆密切相关。这些问题通常可以归类为物理问题。在物理意义上,这些声学问题可能非常复杂;例如,声场可能包含数千个反射分量,或者温度梯度可能以不可预测的方式弯曲声音。与实际问题相反,声音也可以在自由场中考虑,其中其行为非常可预测。在自由场中,分析是直接的。这种分析是有用的,因为它帮助我们理解声波的基本性质。然后,这些基本特征可以适应更复杂的物理问题。
自由场
简单来说,自由场是一个开放的空间。在自由场中,声音沿直线传播且无阻碍。无阻碍的声音不受我们将在后续章节中考虑的许多影响因素的影响。自由场中的声音没有反射、吸收、偏折、衍射、折射、扩散以及共振效应。在大多数实际应用中,这些都是可能(且确实)影响离开声源并传输到听者的声音的因素。近似的自由场可以存在于消声室中,这是一种特殊的房间,所有内部表面都被声音吸收材料覆盖。此外,近似自由场条件可以在声源附近存在。但通常,自由场是一种理论上的构想,是一种允许声音无干扰传播的自由空间。
自由空间不应与宇宙空间混淆。声音无法在真空中传播;它需要像空气这样的介质。在这里,自由空间指的是任何空间,其中声音表现得好像在一个理论的自由场中。在这种独特的环境中,我们可以考虑声音如何从源点发散,以及它的强度如何随距离变化。
声音的发散
考虑图3-1所示的点源,以固定功率辐射声音。由于源的最大尺寸较小(可能是其测量距离的五分之一或更小),因此可以将源视为一个点源。例如,如果源的最大尺寸为1英尺,当距离为5英尺或更远时,可以将其视为点源。从另一个角度看,我们距离声源越远,它就越像一个点源。在自由场中,远离干扰物体的影响,来自点源的声音在各个方向上以球形和均匀的方式传播。此外,正如下文所述,声音的强度随着距离增加而减小。
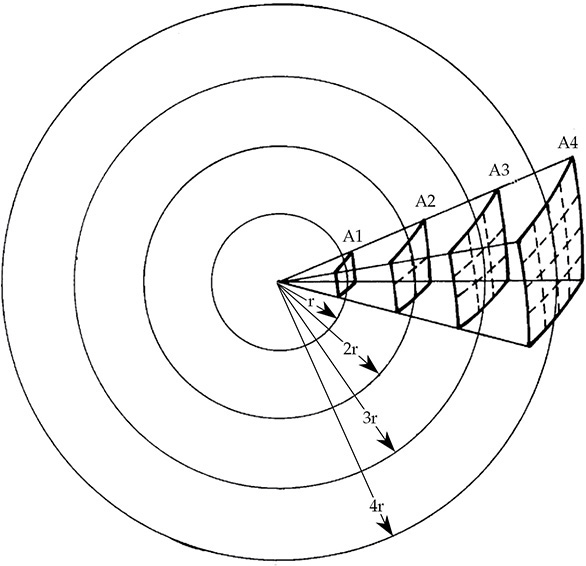
图3-1 在所示的立体角中,随着半径 r 的增加,相同的声能在面积逐渐增大的球面上分布。声音的强度与距离的平方成反比。
在所有方向上,这个声音具有均匀的强度(单位面积的功率)。圆圈代表具有简单倍数半径的球体。通过半径为 r 的小正方形面积 A1 通过的所有声功率也通过半径分别为2r、3r和4r的面积 A2、A3和A4。相同的声功率通过 A1、A2、A3和A4 流出,但是在半径增加时,这个单一方向上的声功率的增量被分散到越来越大的面积上。因此,强度随距离减小。这种减小是由声能的几何扩散引起的,并不是严格意义上的损失。
自由场中的声音强度
在前面的讨论基础上(再次参考图3-1),我们可以观察到理论上的点源发出的声音以球形向外传播。我们还注意到球体的表面积为4πr2。因此,球面上的任何小段的面积也随半径的平方变化。这意味着声音强度(单位面积的声功率)随半径的平方减小。这是一个反比例平方定律。在自由场中,点源声音的强度与距离的平方成反比。换句话说,强度与 1/r2 成正比。更具体地说:
其中,I = 单位面积的声音强度
W = 声源功率
r = 距离源的距离(半径)
在这个方程中,由于 W 和 4π 是常数,我们可以看到将距离从 r 加倍到 2r 会将强度 I 降低为 I/4;这是因为在距离加倍的情况下,声音通过的面积是前一个面积的四倍。同样地,将距离三倍增加会将强度降低为 I/9,将距离四倍增加会将强度降低为 I/16。同样地,将距离从 2r 减半到 r 会使强度增加到 4I。
自由场中的声音压力
声音的强度(单位面积的功率)是一个难以测量的参数。然而,声音压力可以通过使用普通的麦克风等设备轻松测量。在使用声音压力时,自由场方程必须进行修改。因为声音强度与声音压力的平方成正比,所以反比平方定律(对于声音强度)变成了反比距离定律(对于声音压力)。换句话说,声音压力与距离 r 成反比。特别地:
其中,P = 声音压力
k = 一个常数
r = 距离源的距离(半径)
每当距离 r 从声源加倍时,声音压力将减半(而不是减四分之一)。在图3-2中,以分贝为单位绘制了声音压力级与距离的关系。这说明了反比距离定律的基础:当距离声源加倍时,声音压力级减小6 dB。这仅适用于自由场。这个定律为估计许多实际情况下的声音压力级提供了基础。
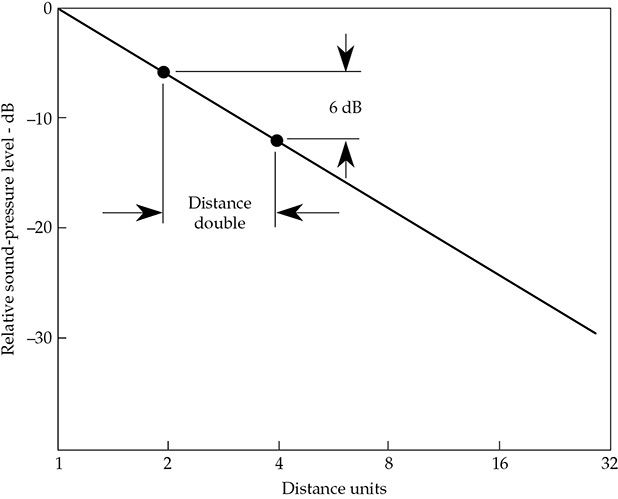
图3-2 声音强度的反比平方定律等于声音压力的反比距离定律。这意味着每当距离加倍时,声音压力级降低6 dB。
自由场中的声音发散
当已知距离 r1 处的声音压力级 L1 来自点源时,可以计算出另一距离 r2 处的声音压力级 L2:
换句话说,两个距离 r1 和 r2 处的声音压力级之差为:
例如,如果在10英尺处测量到80 dB的声音压力级,我们可以确定在15英尺处的声音压力级:
20 log 10/15 = –3.5 dB,级别为 80 – 3.5 = 76.5 dB。
类似地,我们可以确定在7英尺处的声音压力级:
20 log 10/7 = +3.1 dB,级别为 80 + 3.1 = 83.1 dB。
这仅适用于声音呈球面发散的自由场,但在其他条件下,这个方法可能对于粗略估计是有帮助的。
如果一个麦克风距离歌手5英尺,控制室的VU表显示最高值为 +6 dB,将麦克风移动到10英尺处将使读数下降约6 dB。6 dB的数值是近似值,因为这些距离关系只适用于自由场条件。在实际应用中,声音从墙壁反射的影响会导致距离加倍关系小于6 dB。
对这些关系的认识有助于估计声学情况。例如,从10英尺到20英尺的距离加倍,与从100英尺到200英尺的距离加倍一样,在自由空间中都会伴随着相同的声压级下降,即6 dB。这解释了声音在户外传播的巨大传播能力。
即使在远距离,也并非所有声源都像点源一样行为。例如,在繁忙道路上的交通噪音可以更好地建模为多个点源累积作为一条线源。声音在线周围形成一个圆柱体。在这种情况下,声音强度与距离的倒数成反比。将距离从 r 加倍到 2r 会将强度 I 减少到 I/2。这是距离从线源加倍的每个减少 3 dB,或距离从线源减半的每个增加 3 dB。
封闭空间中的声场
在无反射的环境中,封闭空间中存在自由场。然而,在大多数房间中,除了直接声音外,来自周围表面的反射也会影响声音随距离减小的方式。不再有逆方平方定律或逆距离定律来描述整个声场。在自由场中,我们可以根据距离计算声音级别。相反,在完全共鸣的声场中,声音级别在声场中的任何地方都是相等的。实际上,房间呈现出这两个极端的组合,既有直接声音又有反射声音。
例如,假设在一个封闭空间中有一个扬声器,它能在4英尺的距离产生100 dB的声压级。这在图 Fig. 3-3 中显示出来。在离扬声器非常近的区域,声场处于相当混乱的状态。在如此近的距离下,扬声器不能被视为点源。这个区域称为近场。在近场中,声级在每次距离加倍时减少约12 dB。这个近场区域(不要与“近场”或“近距离”工作室监听混淆)在实际应用中具有有限的实用价值。
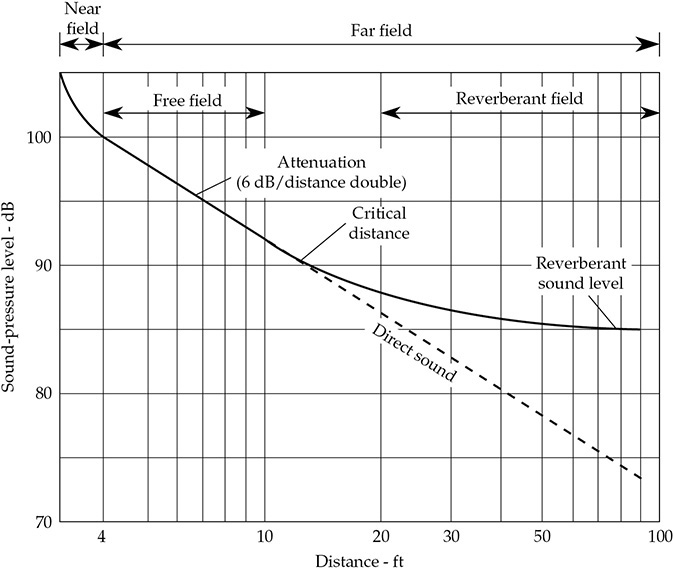
FIGURE 3-3 即使在封闭空间中,靠近源头的位置仍存在近似自由场,声压级在每次距离加倍时会减弱6 dB。按定义,临界距离是直接声压级等于混响声压级的距离。离源头更远的地方,声压级保持恒定,并取决于房间中的吸声量。
在远离扬声器的地方,可以进行重要的测量。远场由自由场、混响场和它们之间的过渡区域组成。在靠近扬声器的地方,近似自由场条件存在,扬声器起作为点源的作用。直接声音占主导地位,在这个有限空间中呈球形散射,表面的反射声音相对较低。在这个区域中,声压级在每次距离加倍时降低6 dB。
远离扬声器时,来自房间表面的反射声音会影响结果。我们将临界距离定义为房间中直接声音和反射声音级别相等的位置。临界距离在对环境声学进行粗略的单一数值描述时非常有用。距离源头更远的地方,混响声场占主导地位。其声级保持恒定,即使距离源头更远。这个声级取决于房间中的吸声量。例如,在一个吸声性很高的房间中,混响水平会很低。
半球形场和传播
真正的球形发散需要没有反射表面的存在。由于这很难实现,有时会通过将声源(如扬声器)放置在坚硬的反射表面上,近似实现。这样可以创建一个向上辐射的半球形声场。例如,可以用于测量扬声器的响应。在这种情况下,声场辐射到一个面积为2πr2的表面上。因此,强度变化为I = W/2πr2。与球形声场一样,在半球形声场中,声压级在每次距离加倍时会减弱6 dB。然而,在半球形声场中,声级开始时比球形声场高3 dB。
我们如何表征声波在地球表面上的半球形传播呢?根据“每次距离加倍6 dB”的规则进行的估计只是粗略的近似值。在户外,来自地面的反射通常会使声级随距离而降低,降低幅度小于6 dB的近似值。地球表面的反射效率因地而异。考虑距离源头10英尺和20英尺处的声级。在实践中,两者之间的差异可能更接近4 dB而不是6 dB。对于这样的户外测量,必须按照“每次距离加倍4或5 dB”的规则进行。一般环境噪声也可能影响特定声源的测量。
要点
• 自由场可以被视为开放空间;声音直线传播且不受阻碍。
• 理论上的点源发出的声音呈球形向外传播。
• 在自由场中,声强(单位面积上的声功率)按照半径的平方进行衰减。这符合反比例平方定律。
• 在自由场中,当距离源头加倍时,声压级下降6 dB。这符合反距离定律。
• 在封闭空间中,除了直接声音之外,来自封闭表面的反射会影响声音随距离的衰减方式。
• 临界距离是房间内直接声音和反射声音级别相等的位置。



