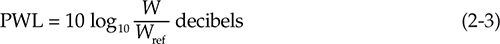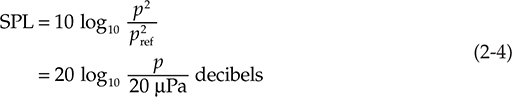《声学手册(第七版)》第二章

章节 2

声级和分贝

分贝是音频领域中最重要的测量单位之一。分贝提供了一种非常有效的方式来描述音频现象及我们对其的感知。在本章中，我们将探讨分贝的概念，并了解如何使用分贝来测量不同应用中的声级。通过几个数值示例，演示使用分贝测量所需的数学计算。

以分贝表示的声级清晰地展示了人类听觉的广泛灵敏度范围。听觉阈限与空气中可感知声音的最低限度相匹配，也就是未受干扰的空气分子撞击鼓膜所产生的噪声。在声级范围的另一端，耳朵可以容忍高强度的声级；在非常高的强度下，听力损伤是一种非常真实的可能性。以分贝表示的声级是处理耳朵对声压灵敏度的十亿倍声压范围的便捷方式。

比率与差异

有无数种方法来测量任何现象的变化。例如，我们可以将变化表示为绝对差异，也可以使用比率。哪种方式更适合表示声音的感知响度变化呢？

想象一个声源设置在完全受保护免受干扰噪声的房间中。调整声源的音量为1单位的弱音，并仔细记录其响度。在观察A中，要使感知的响度翻倍，声压必须从1增加到10单位。此时声源的压力调整为10,000单位。对于观察B，要再次使感知的响度翻倍，我们发现声压必须从10,000增加到100,000单位。该实验的结果可以总结如下：

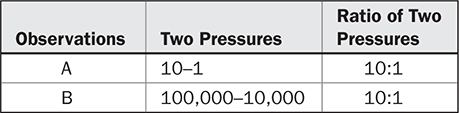
观察A和B实现了相同的响度翻倍。在观察A中，这是通过声压仅增加9单位来实现的，而在观察B中，则需要增加90,000单位。我们得出结论，压力的比率似乎比压力的绝对差异更能描述响度的变化。

早期声学研究者，包括恩斯特·韦伯、古斯塔夫·费希纳和赫尔曼·冯·赫尔姆霍兹，证明了在此类测量中使用比率的重要性。比率同样适用于视觉、振动甚至电击的感觉。与刺激的绝对差异相比，刺激的比率更接近人类的感知。尽管匹配并不完美，但足够接近，足以有力地支持使用以比率为基础的分贝来表示声级。

功率比、强度比、声压比、电压比、电流比或任何其他比率都是无量纲的。例如，1瓦与100瓦的比率为1瓦/100瓦，分子中的瓦单位和分母中的瓦单位相互抵消，留下一个没有单位的纯数。这在我们讨论分贝时非常重要，因为分贝使用对数，而对数只能应用于无量纲数。

数字表示

表2-1展示了数字可以表示的三种不同方式。十进制和算术形式在日常活动中很常见。指数形式虽然不太常用，但几乎具有简化许多关系表达的独特能力。当我们写"一十万"瓦特时，可以将数字表示为100,000 W或10⁵ W。当我们写"一万亿分之一"瓦特时，小数点后的一串零显得笨拙，但写10^-12 W很容易。工程计算器以科学记数法的指数形式显示，可以表示非常大或非常小的数字。此外，前缀皮可表示10^-12，所以该值可以表示为1皮瓦（稍后在表2-4中显示）。

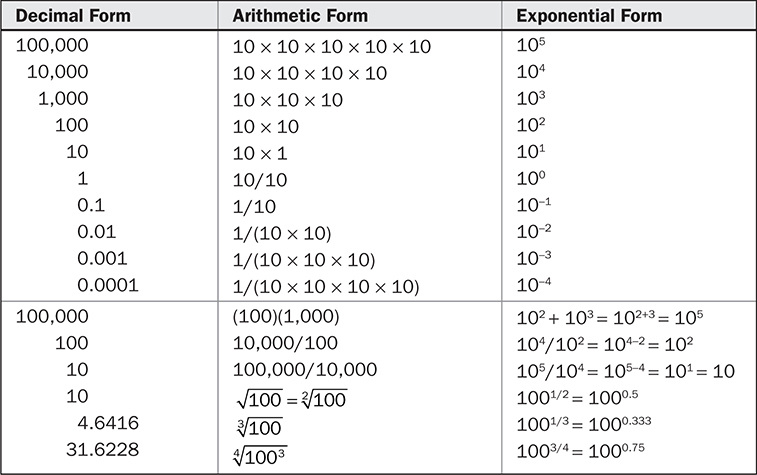
TABLE 2-1 十进制、算术和指数形式的数字表示

我们能够听到的最轻微声音强度（听觉可察觉阈限）约为10^-12 W/m²。非常响亮的声音（引起疼痛感）可能达到10 W/m²。（声强是指定方向上单位面积内的声功率。）从最轻微的声音到极响的声音，强度的范围为10,000,000,000,000。显然，将这个范围表示为指数形式10¹³更为方便。此外，将强度10^-12 W/m²作为参考强度I_ref，并将其他声音强度I表示为相对于该参考的比值I/I_ref，也是非常有用的。例如，声音强度10^-9 W/m²可以写作10³或1,000（该比值是无量纲的）。我们可以看到，10^-9 W/m²是参考强度的1,000倍。

对数

将100表示为10²简单地意味着10 × 10 = 100。同样，10³表示10 × 10 × 10 = 1,000。但是267怎么表示呢？这就是对数的用处。对数是比例数，而对数尺度是一种按比例标定的尺度。我们一致认为100等于10²。根据定义，我们可以说以10为底的100的对数等于2，通常写作log₁₀100 = 2，或者简单地写作log 100 = 2，因为常用对数是以10为底。数字267可以表示为介于2和3之间的某个幂的10。避免进行数学计算，我们可以使用计算器输入267，按下"log"按钮，然后显示出2.4265。因此，267 = 10^2.4265，log 267 = 2.4265。对数非常方便，因为正如表2-1所示，它们将乘法简化为加法，将除法简化为减法。

对数对音频工程师特别有用，因为它们可以将测量结果与人类听觉相关联，并且还可以高效地表示大范围的数字。对数是以分贝形式表示声级的基础，其中声级是两个类似功率的比率的对数。特别地，以分贝表示的声级是以10为底的对数乘以10，描述如下。

分贝

我们注意到以比率的形式表示声强是有用的。此外，我们可以将声强表示为比率的对数。声强 I 可以根据参考强度 I_ref 表示如下：

声强的测量是无量纲的，但为了明确其值，我们赋予其贝尔（取自亚历山大·格雷厄姆·贝尔¹译注：https://en.wikipedia.org/wiki/Alexander_Graham_Bell）作为单位。然而，以贝尔为单位时，值的范围相对较小。为了使用更方便，通常我们使用分贝来表示数值。分贝（dB）是贝尔的1/10。一个分贝是以10为底的对数乘以10，作用于两个强度（或功率）的比率。因此，以分贝表示的声强比率变为：

这个值被称为声强级（以分贝为单位），它与声强（I，以瓦特/平方米表示）不同。使用分贝很方便，分贝值更接近于我们对声音响度的感知方式。

有时需要用分贝来表示除了强度之外的级别，这时等式（2-2）同样适用于声强、声功率、电功率或任何其他类型的功率。例如，我们可以将声功率级表示为：

其中 PWL = 声功率级，以分贝为单位

     W = 声功率，瓦特

  W_ref = 参考功率，10^–12 W

声强难以测量。在声学中，声压通常是最易测量的参数（就像电路中的电压一样）。因此，经常使用声压级（SPL）。SPL是声压的对数值，就像声强级（IL）对应于声强一样。SPL与IL大致相等；它们通常都称为声级。声强（或功率）与声压的平方成正比。这会略微改变我们使用的定义方程。当参考压力为20微帕（μPa，微帕斯卡）时，以微帕（μPa）或其他单位测量的声压 p 的SPL为：

其中 SPL = 声压级，以分贝为单位

          p = 声压，微帕或其他单位

       p_ref = 参考声压，微帕或其他单位

表2-2的列示了方程（2-2）或（2-3），以及方程（2-4）的使用情况。

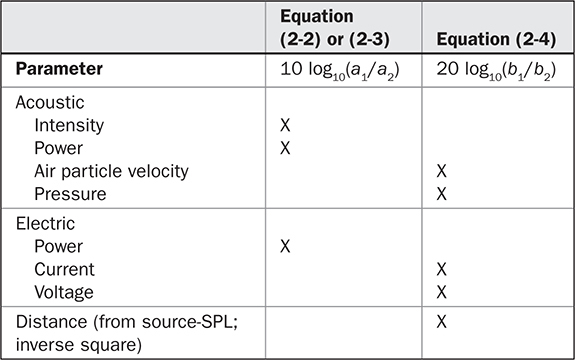
表2-2 使用10 log和20 log方程

参考级别

正如我们所见，参考级别被广泛用于建立测量的基准。例如，声级计用于测量特定的声压级。如果相应的声压级以常规的压力单位表示，将得到一系列非常大和非常小的数值。如前所述，通过以分贝表示级别，我们将大和小的比例压缩到一个更便于使用和理解的范围内。基本上，声级计的读数是一定的声压级，即20 log (p/p_ref)，如方程（2-4）所示。声压参考 p_ref 必须标准化，以便进行直接比较。多年来已经使用了几种这样的参考压力，但对于空气中的声音，标准参考压力是20 μPa。这与参考压力0.0002微巴或0.0002达因/厘米²看起来可能相差很大，但实质上它们只是以不同的单位书写的相同标准。这是一个非常小的声压（0.0000000035磅/平方英寸），与1 kHz时人耳的听觉阈值非常接近。声压（以帕斯卡、磅/平方英寸表示）和声压级之间的关系如图2-1所示。

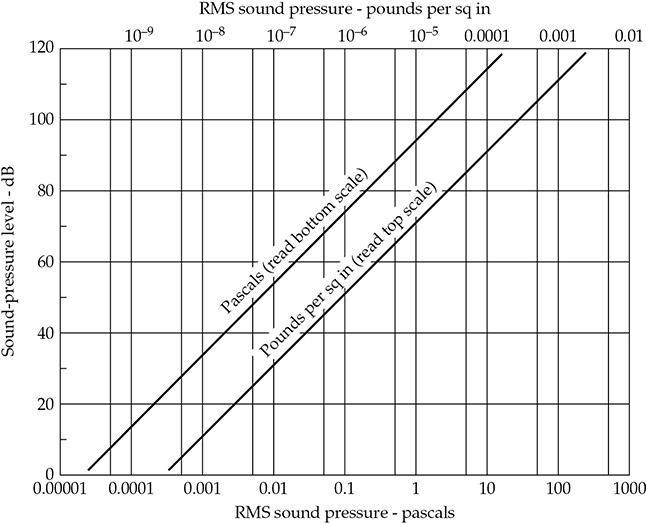
图2-1 这个图显示了声压（以帕斯卡或磅/平方英寸表示）与声压级（参考为20 μPa）之间的关系。这是解方程（2-2）的图形方法。

当遇到类似“声压级为82 dB"的陈述时，82 dB的声压级通常用于与其他级别直接比较。然而，如果需要声压，可以通过从方程（2-4）反推计算，如下所示：

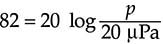
计算器上的 y^x 按钮帮助我们计算10^4.1。输入10，输入4.1，按下 y^x 按钮，就会出现值 12,589。

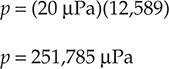
这里还有另一个教训。82有两个有效数字。251,785有六个有效数字，并暗示了一种不存在的精度。仅仅因为计算器上这样显示，并不意味着确实如此。更好的答案是252,000 μPa，或0.252 Pa。

对比对数形式和指数形式

可以从表2-1中看出，数值表达的对数形式和指数形式是等价的。在使用分贝时，理解这种等价性非常重要。

假设我们有一个功率比为5：

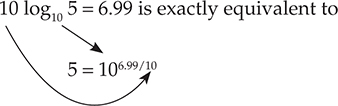
指数表达式中有两个10，但它们来自不同的源，如箭头所示。现在让我们来看一个声压比为5：

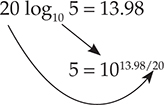
请记住，空气中的声压级意味着压力比中的参考压力 (p_ref) 为20 μPa。还有其他参考量；一些常见的参考量列在表2-3中。当处理非常小和非常大的数值时，通常会使用表2-4中的前缀。这些前缀是希腊语中10的幂的名称。

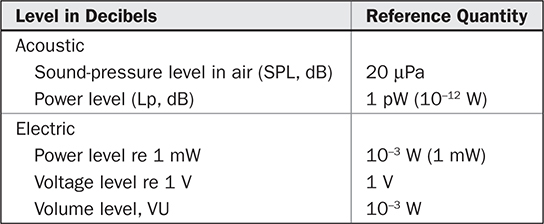
表2-3 常用参考量

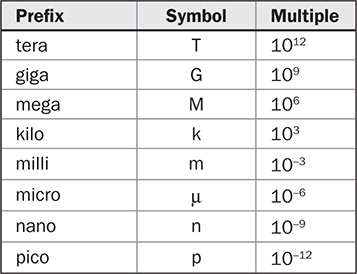
表2-4 前缀、符号和幂次

声功率

产生非常响亮的声音并不需要很多瓦特的声功率。这对于音乐播放来说是幸运的，因为扬声器的效率（给定输入产生的输出）非常低，可能在10%左右。另一方面，为了获得更高的声级，增加放大器功率可能会令人沮丧。将放大器功率从1 W增加到2 W相当于功率级增加了3 dB（10 log 2 = 3.01），但这只会带来非常小的音量增加。类似地，将放大器功率从100 W增加到200 W或从1,000 W增加到2,000 W也会带来相同的3 dB声级增加。

表2-5列出了各种声音的声压和声压级。声压从0.00002 Pa（20 μPa）到100,000 Pa之间存在巨大差异，但当以声级形式表示时，这个范围被压缩为一个便于处理的形式。同样的信息以图形形式呈现在图2-2中。

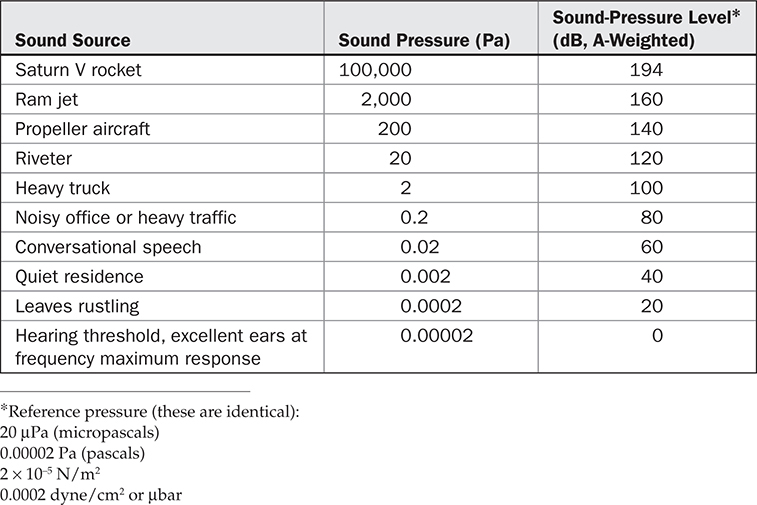
表2-5 声压和声压级的示例

图2-2 通过与已知声音的比较，可以了解1 Pa声压的相对大小。空气中声音的标准参考压力为20 μPa，与最低可听压力非常接近。

火箭Saturn V的发射声压级为194 dB（发射期间声压级可能更高）。 （作为对比，以10英尺距离引爆50磅的TNT也会产生类似的声压级）。该声压级接近大气压，因此在大气压的数量级上产生干扰。194 dB的声压是一个均方根（RMS）值。峰值声压大约为其1.4倍，可以完全调制大气压。

使用分贝

正如我们所见，声级是两个类似功率的量的比值的对数表示。当计算声级时，除功率比值外，还遵循一定的约定。方程式（2-4）中的约定是声功率与声压的平方成正比。放大器的电压级增益以分贝表示为20 log (输出电压/输入电压)，这适用于输入和输出阻抗不同的情况。然而，对于功率级增益，如果阻抗不同，就必须考虑阻抗。重要的是明确指出所需的是哪种级别，或者将级别增益标记为“相对增益，分贝"。以下示例说明了分贝的使用。

示例1：声压级 声压级为78 dB。声压是多少？

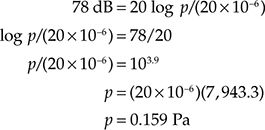
请注意，SPL测量中的参考级别为20 μPa。

示例2：扬声器声压级 将1 W输入8Ω的扬声器在1 m（3 ft）处的轴向输出声压级（SPL）为115 dB。在6.1 m（20 ft）处的SPL是多少？

20 log 6.1因子的假设是扬声器在自由场中工作，并且在这种情况下反比例平方定律是有效的。如果扬声器远离反射表面，则对于20英尺的距离来说，这是一个合理的假设。自由场在第3章中有更详细的描述。

这个扬声器的SPL在1 m处为115 dB，输入功率为1 W。如果将输入功率从1 W降低到0.22 W，那么在1 m距离处的SPL是多少？

请注意，由于比较的是两个功率，因此使用10 log。

示例3：麦克风电压 一个全向动圈麦克风的开路电压在150Ω情况下为-80 dB。还规定0 dB = 1 V/μbar。开路电压ν是多少伏特？

示例4：线路放大器输出电压 一台线路放大器的输入阻抗为600Ω，输出阻抗为600Ω。它的增益为37 dB。如果输入为0.2 V，输出电压是多少？

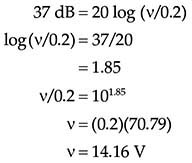
示例5：通用放大器增益 一台放大器的桥接输入阻抗为10,000Ω，输出阻抗为600Ω。使用50 mV输入时，观察到1.5 V的输出。放大器的电压增益是多少？

需要注意的是，由于阻抗的差异，这不是功率级增益。然而，在某些情况下，计算电压增益可能有实际用途。

示例6：音乐厅计算 音乐厅中的一个座位距离定音鼓84英尺。定音鼓击奏一个音符。在座位上测量到的音符的直接声音的声压级为55 dB。来自最近侧墙的第一个反射声在直接声音到达后105毫秒到达座位。（A）反射声音到达座位的距离是多少？（B）假设墙壁上的反射完全，反射在座位的声压级是多少？（C）直接声音到达座位后，反射将被延迟多长时间？

（A）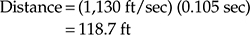

（B）首先，必须估计离定音鼓1英尺的声级L：

反射在座位的声压级为：

(C) 反射声音在到达座位后会延迟：

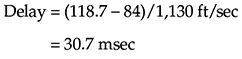
这里也假设自由场。30.7毫秒的反射可能被称为初级回声。

示例7：组合分贝 一间工作室有一个暖通空调（HVAC）系统和一个地面立式风扇。如果HVAC和风扇都关闭，则存在非常低的噪声水平，可以在这个计算中忽略不计。如果只有HVAC在运行，则给定位置的声压级为55 dB。如果只有风扇在运行，则声压级为60 dB。如果两者同时运行，声压级将是多少？答案肯定不是55 + 60 = 115 dB。相反，

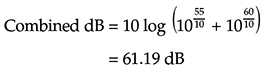
我们可以看到，55 dB的声级仅略微增加了60 dB声级所建立的整体声压级。

在另一个示例中，如果两个噪声源的组合级别为80 dB，并且关闭其中一个源的级别为75 dB，则剩余源的级别是多少？

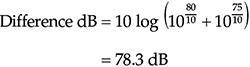
换句话说，将78.3 dB级别与75 dB级别组合，得到的组合级别为80 dB。假设HVAC和风扇都产生宽带噪声信号。重要的是要记住，只有当声音具有相同或类似的频谱特性时，才能比较不同的声级。

测量声压级

声级计旨在提供声压级（SPL）的读数。声压以分贝为单位，参考标准参考级为20微帕（μPa）。人类的听觉反应在音频频段上并不是平坦的。例如，我们的听觉敏感性在低频和高频时特别下降。而且，这种下降在较低的音量级别下更加明显。因此，为了模拟人类听觉，声级计通常提供了被称为A、B和C的加权网络的选择，其频率响应如图2-3所示（图2-3）。这些网络在低频和高频时降低了测量的声压级。A网络是40听音响应的倒转，B网络是70听响应的倒转，C网络是100听响应的倒转。听音（phon）在第4章中有详细描述。根据待测声音的一般级别（背景噪声、喷气发动机等），选择特定的加权网络。例如：

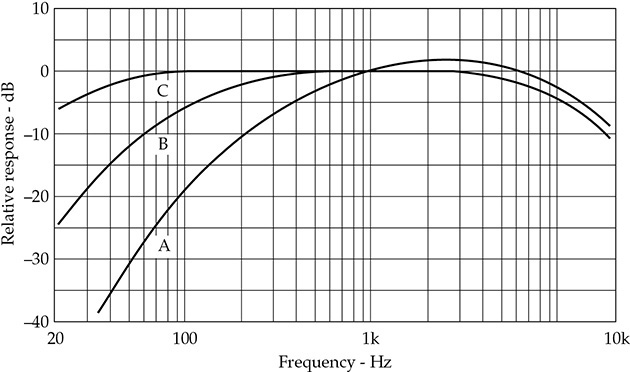
图2-3 声级计的A、B和C加权响应特性。最常用的是A加权。

• 对于20至55 dB的声压级，请使用A网络。

• 对于55至85 dB的声压级，请使用B网络。

• 对于85至140 dB的声压级，请使用C网络。

这些加权网络响应曲线的设计目的是使声级计的读数更加符合声音的相对响度。然而，B和C加权常常与人类的感知不一致；不再推荐使用B加权。Z（零）加权描述了平坦的频率响应，该标准在IEC 61672中有描述。A加权在包括环境测量在内的许多声学噪声测量中被广泛使用。当使用A加权进行测量时，该值被标记为dBA或dB(A)。在使用校准麦克风进行dBA测量时，dB SPL单位参考为20μPa = 0 dB SPL。通常情况下，dBA的读数要低于未加权的dB读数。由于A加权在1 kHz以上基本平坦，dBA和未加权读数之间的任何差异主要显示信

号的低频内容的差异。例如，读数的较大差异表明信号具有显著的低频内容。IEC 61672标准中也描述了A加权网络。

这些简单的频率加权无法准确表示响度。使用简单加权进行的测量不被接受为测量响度级别，而仅用于级别比较。建议使用八度频带或1/3八度频带进行声音的频率分析。更高级的测量技术在附录A中有描述。

正弦波测量

正弦波（或正弦信号）是一种特定类型的交替信号，具有一组特定的术语描述。在示波器上观察，最容易读取的值是峰峰值（电压、电流、声压或正弦波表示的任何量），如图2-4所示。如果波形是对称的，则峰峰值是峰值的两倍。

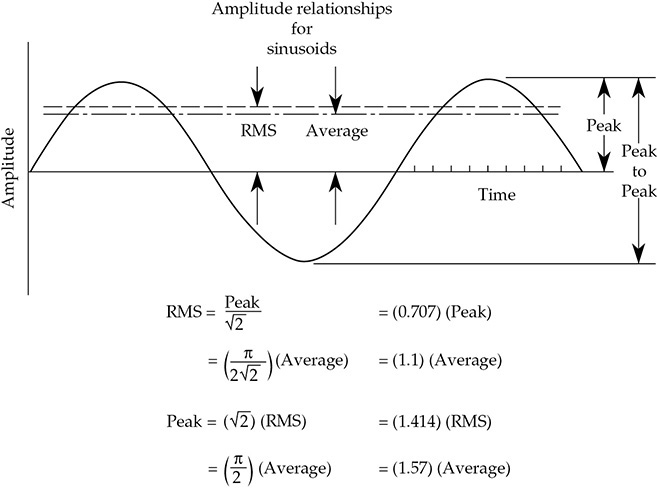
图2-4 正弦波的幅度关系适用于电压或电流的正弦波，以及声压等声学参数。音频领域中使用的另一个术语是峰值因子，即峰值除以RMS。这些数学关系适用于正弦波，并不能应用于复杂的波形。

常见的交流（交流电）电压表实际上是一个直流（直流电）仪表，配有将交变正弦波电流变为脉动单向电流的整流器。然后，直流表显示平均值，如图2-4所示。然而，这样的仪表几乎普遍校准为RMS（均方根，如下所述）。对于纯正弦波，这是一种相当可接受的假设，但对于非正弦波形，读数将有误差。

1安培（A）均方根（RMS，或有效值）的交流电在发热功率上与1安培的直流电完全等效，因为它通过已知阻值的电阻。毕竟，无论交流电流流动方向如何，它都可以加热电阻器或进行工作；只是一个评估问题。在图2-4的右侧正曲线中，为了每个标记的时间增量，读取纵坐标（线与曲线之间的高度）。然后，（a）将这些纵坐标值的平方，（b）将平方值相加，（c）找到平均值，（d）对平均值进行平方根运算。对这个平均值开平方根得到图2-4正曲线的RMS（均方根）值。对于

负曲线也可以进行同样的操作（负纵坐标的平方给出正值），但对于对称波形，直接将正曲线翻倍更容易。通过这种方式，可以确定任何交替或周期波的RMS或“发热功率"值，无论该波表示电压、电流还是声压。图2-4还提供了仅适用于正弦波的关系摘要。重要的是要记住，简单的数学关系正确地描述了正弦波，但不能应用于复杂的声音。

电气、机械和声学的类比

声学系统（例如扬声器）可以用等效的电气或机械系统来表示。工程师使用这些类比来建立分析给定系统的数学方法。例如，通过将封闭空间中的空气视为电路中的电容器，吸收和释放振膜运动所传递的能量，可以澄清机柜对扬声器功能的影响。

图2-5显示了电气、机械和声学系统中三个基本元素的图形表示。电路中的电感相当于机械系统中的质量和声学系统中的惯性。电路中的电容类比于机械系统中的顺应性和声学系统中的电容。电阻在这三个系统中都是电阻，无论是玻璃纤维中对空气粒子运动的摩擦损耗，轮轴承中的摩擦损耗，还是电路中电流流动的阻力。

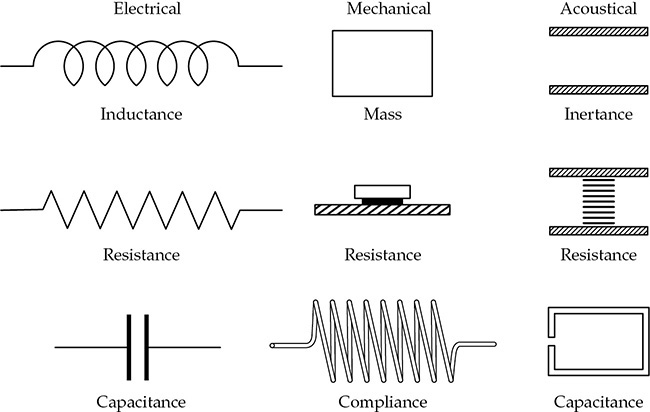
图2-5 电气系统中的三个基本元素及其在机械和声学系统中的类比。

要点

• 在许多情况下，使用比率和对数来更接近地将声学测量与人类听觉相关联。

• 分贝可以用来表示声强和其他现象，作为比值的对数。

• 声压级（SPL）是声压的对数值；根据用途，使用稍有不同的方程来定义它。

• SPL测量是相对于参考级别进行的，例如20μPa。

• 为了更符合人类感知，SPL测量通常会使用特定的加权响应曲线。常用的是A加权曲线。

• 许多正弦波测量使用一组特定的关系描述，但这些关系不能应用于复杂的波形。