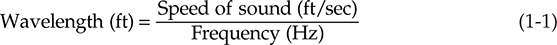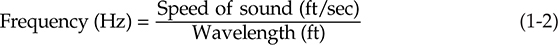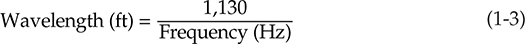《声学手册(第七版)》第一章
章节1
声学基础
声音可以被视为空气或其他弹性介质中的波动。在这种情况下,声音作为信号的激励。声音也可以被视为听觉机制的激发,导致其感知。在这种情况下,声音是一种感觉。这两种性质常见于音频(信号)处理和音乐两个领域。不同问题使用不同的方法。如果我们对房间中空气的物理扰动感兴趣,这是一个物理问题。如果我们对一个人在房间中听到的扰动是如何感知的感兴趣,必须使用心理声学方法。因为本书涉及与人相关的声学问题,所以声音的两个方面都将被考虑。话虽如此,由于我们主要关注房间材料和几何形状对扰动的影响,我们的研究主要涉及物理学。
声音可以通过客观现象进行表征。例如,频率是声音的客观属性;它指定了每单位时间(通常为1秒)内波形的重复次数。频率可以很容易地在示波器或频率计上测量。从物理学的角度来看,频率的概念很直观。我们将着重于探索声音的客观特性,特别是在声音的属性是如何由我们所居住的房间所决定的方面。
另一方面,重复的频率可以以主观方式进行表征。频率被(人耳)感知为音高,这是声音的主观属性。感知上,我们对轻柔和响亮的100 Hz频率可以听到不同的音调。对一定频率的纯音,低频纯音的音调随声强增加而下降,高频纯音的音调却随强度增加而上升。Harvey Fletcher发现,以适度的强度播放168 Hz和318 Hz的纯音会产生一种非常不和谐的声音。¹译注:可能指等响曲线实验然而,当强度很高时,耳朵会将在150 Hz到300 Hz的八度关系中的纯音听作愉悦的声音。我们不能将频率和音高等同起来,但它们是类似的。强度和响度之间也存在着客观/主观的二重性。同样,波形(或频谱)与感知品质(或音色)之间的关系也不是线性的。复杂的波形可以用基频和一系列振幅和相位不同的谐波来描述。但是音色的感知受到频率-音高相互作用以及其他因素的复杂影响。
声音的物理属性与我们对其的感知之间存在着微妙而复杂的相互作用。正是音频和声学中的这种复杂性创造了如此有趣的问题。一方面,设计扬声器或音乐厅应该是一个简单而客观的工程过程。但实际上,这种客观专业知识必须与纯主观的智慧谨慎地结合起来。正如经常被指出的那样,扬声器的设计并不是为了将正弦波播放到放置在无混响室中的校准麦克风中。相反,它们被设计为在我们的听音室中播放音乐。换句话说,音频和声学的研究涉及艺术和科学两个方面。为了了解音频和声学的复杂性,我们从学习声音科学开始,但要牢记我们的耳朵最终决定了我们的项目的成败。
简谐振动和正弦波
图1-1中的弹簧和质量构成了一个振动系统。此外,重物以简谐振动的方式移动。当重物静止时,系统处于平衡状态。如果将重物拉向负5标记并释放,弹簧将把重物拉回0位置。然而,重物不会停在0位置;其惯性将使其超过0位置,几乎达到正5位置。重物的位移定义了振动的振幅。
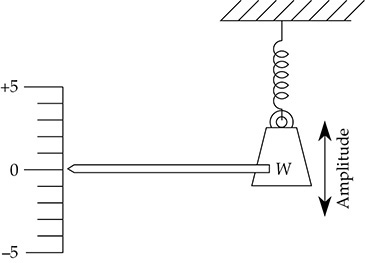
图1-1:由于弹簧的弹性和重物的惯性,弹簧上的重物以其固有频率进行振动。
重物将继续振动或做周期性的运动。每次上下摆动被称为一个周期,这种运动被称为周期性运动。在质量和弹簧的组合中,弹簧的弹性和重物的惯性使得振动或周期性运动成为可能。弹性和惯性是介质传递声音的必备特性。在这个例子的实际情况中,由于弹簧和周围空气的摩擦损耗,振动的振幅将会逐渐减小。
简谐振动是一种基本的振动运动,它在声音和电子学中呈现出同样基本的波形。为了说明这一点,在图1-2中所示,如果将一支笔固定在重物的指针上,并以均匀的速度将一条纸移动过去,那么所得到的轨迹就是一个正弦波。正弦波是与简谐振动密切相关的纯净波形。在这个图中,由笔追踪的正弦波已经完成了一个完整的周期,并且已经超过了第二个周期的一半。(暂时忽略会减小振幅的摩擦损耗。)重物的周期性运动将持续无限地追踪这个正弦波。(在没有外力的情况下,这个系统不会有其他运动。)不管怎样,这个显示振幅与时间关系的正弦波图形都是绘制许多不同的波形的基础。
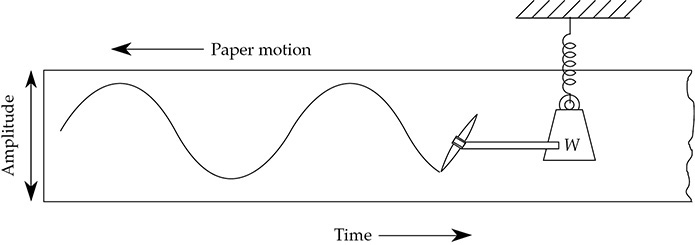
图1-2:固定在振动重物上的笔在以均匀速度移动的纸带上追踪出正弦波。这展示了简谐振动与正弦波之间的基本关系。
作为振动运动的另一个例子,考虑一辆内燃汽车发动机中与曲轴相连的活塞。曲轴的旋转和活塞的上下运动展示了旋转运动与线性简谐振动之间的关系。与弹簧上的重物一样,将活塞位置绘制为时间的函数会产生一个正弦波。
介质中的声音
前面的例子中的重物和弹簧系统模拟了空气分子的运动。如果一个空气粒子被位移出其原始位置,空气的弹性力将试图将其恢复到原始位置。由于粒子的惯性,它会超过静止位置,引发相反方向的弹性力,依此类推。
弹性介质对声波的存在至关重要。因为空气是声音传导的常见媒介,所以人们很容易忽视其他介质也是声音的传导者。如此,声音可以很容易地在气体、液体和固体中传导,如空气、水、钢铁、混凝土等,它们都是弹性介质。想象一下铁轨:一个站在远处的朋友用石头敲击一根铁轨。你会听到两种声音,一种声音通过铁轨传来,一种通过空气传来。通过铁轨传来的声音会比通过空气传来的声音先到达,因为钢铁中声音的传播速度比空气中的快。同样,液体可以是非常有效的声音传导介质——水下的声音可以经过数千英里的海洋传播后被检测到。
没有介质,声音就无法传播。在实验室中,一个电动蜂鸣器悬挂在一个厚重的玻璃罩内。当按下按钮时,可以清楚地听到蜂鸣器的声音。当将空气抽出玻璃罩时,声音逐渐变得微弱,直到听不见为止。传导声音的介质——罩子内的空气已经在源和耳朵之间被移除。外太空是一个几乎是真空的环境,除了宇宙飞船或航天服内的微小大气层,声音无法传导。
粒子运动
风产生的波浪穿过一片麦田,但随着波浪的行进,单个秸秆仍牢牢扎根。类似地,传播声波的空气粒子并不远离它们的静止位置,如图1-3所示。扰动在传播,但传播的粒子仅在局部区域内运动(最大位移可能只有几万分之一英寸)。还要注意,粒子的速度在其平衡位置最大,在最大位移处速度为零(摆锤也具有相同属性)。最大速度被称为速度振幅,最大位移被称为位移振幅。最大粒子速度非常小,即使对于响亮的声音也小于0.5英寸/秒。正如我们将看到的,要降低声音的强度,我们必须降低粒子的速度。²译注:后文会提到粒子速度与响度的关系。
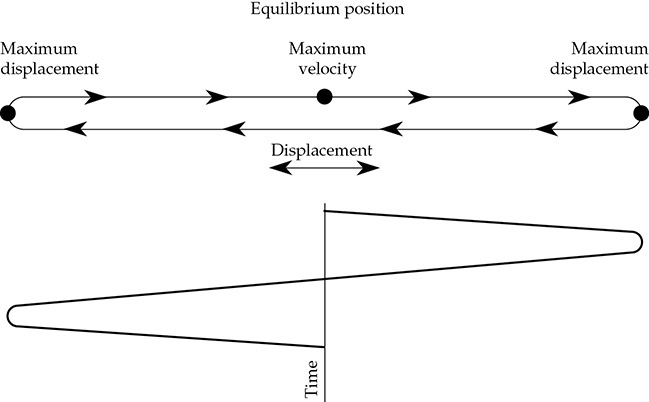
FIGURE 1-3 通过经过的声波的能量,空气粒子被迫绕其平衡位置振动,这是由于空气的弹性力和空气粒子的惯性的相互作用。
粒子运动有三种明显的形式。对于在空气等气体介质中传播的声音,粒子沿着声音传播的方向运动。这种运动被描述为纵波,沿传播方向膨胀和收缩,如图1-4A所示。如我们将看到的,这种振动会导致高压区和低压区。在压力最小值的两侧,瞬时压力极性相反。一侧的压力正在增加,而另一侧的压力正在降低。第二种波动形式由小提琴弦示例,如图1-4B所示。弦的微小元素以横向方式移动,即与弦上波沿着的方向垂直。第三种形式是,如果在平静的水面上投掷一块石头,同心波从冲击点传播出去,水粒子沿圆形轨道运动(至少对于深水来说),如图1-4C所示。
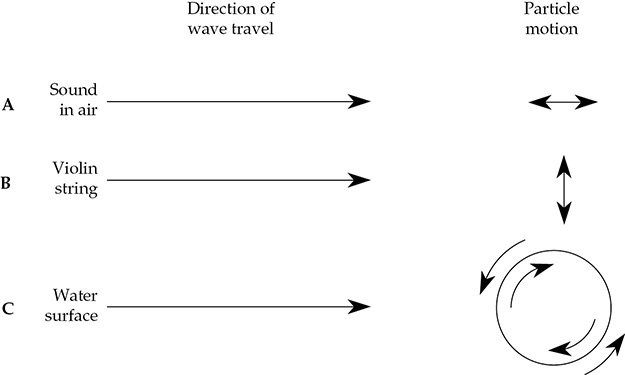
FIGURE 1-4 参与声波传播的粒子可以沿(A)空气中的纵向运动,(B)弦上的横向运动,或者(C)水面上的圆形运动。
声音的传播
空气粒子如何轻微前后移动,能够将音乐从扬声器传送到我们的耳朵?图1-5中的点代表具有不同密度变化的空气分子。密集在一起的分子代表压缩区域(波形的波峰),其中的气压略高于大气压力(通常海平面上约为14.7磅/平方英寸)。稀疏区域代表稀疏区域(波形的波谷),其中的压力略低于大气压力。箭头(见图1-5)表示,平均而言,分子在压缩波峰的右侧移动,并在波峰之间的稀疏区域中向左移动。由于弹性,任何给定的分子在初始位移后,将回到其原始位置。随着声波向右均匀传播,它将向右移动一定距离,然后向左移动大致相同的距离,以保持其静止位置。声音的传播是通过从一个粒子向另一个粒子的动量传递而实现的。
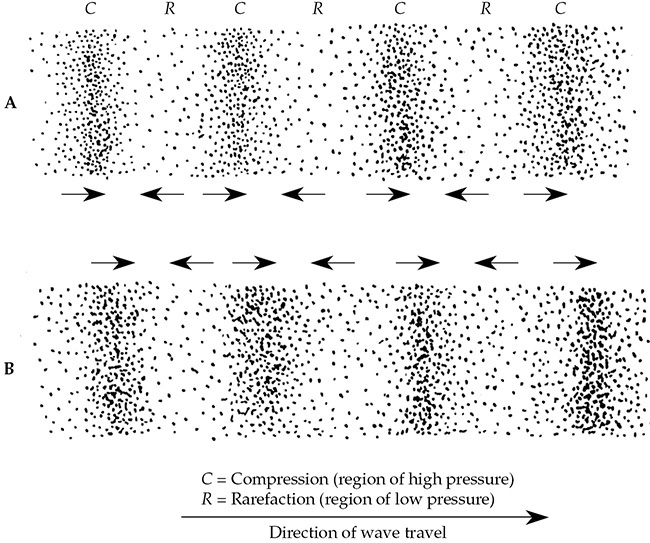
FIGURE 1-5 声波通过介质传播时改变局部空气粒子的密度。(A)声波使空气粒子在某些区域被挤压在一起(压缩),在其他区域散开(稀疏)。 (B)一瞬间后,声波向右稍微移动。
在这个例子中,为什么声波向右传播?答案可以通过仔细观察箭头(见图1-5)得出。当两个箭头指向彼此时,分子倾向于聚集在每个压缩区域的右侧一点。当箭头指向彼此相反时,分子的密度降低。因此,较高压力的波峰和较低压力的波谷的运动解释了声波向右传播的过程。
如先前提到的,波峰处的压力高于大气压力,波谷处的压力低于大气压力,如图1-6的正弦波所示。这些压力的波动非常微小。人耳能听到的最微弱的声音(20 μPa)的压力比大气压力小约5,000亿倍。总结一下,典型的声音(如语音和音乐)在大气压力上叠加了相应小的压力波动。
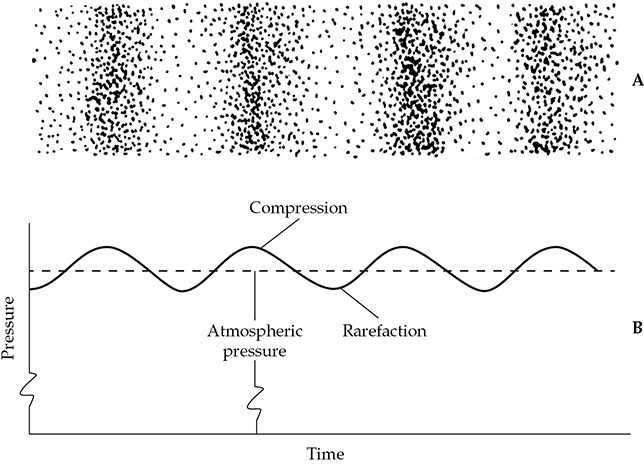
FIGURE 1-6 声波的压力变化叠加在大气压力上。(A)在空气中压缩和稀疏区域的瞬时视图。(B)压缩区域略高于大气压力,稀疏区域略低于大气压力。
声音的速度
空气中的声音速度在摄氏21度(华氏70度)约为344米/秒(1,130英尺/秒)。这大约相当于770英里/小时(1,239公里/小时)。在空气动力学领域,这个速度被称为马赫1.0(通常指当地空气中声音传播速度)。与我们熟悉的事物相比,这个速度并不算快。例如,商用飞机通常以接近音速的速度飞行;如波音787喷气式客机的巡航速度为561英里/小时(马赫0.85)。声音的速度比光的速度(670,616,629英里/小时)慢得多。声音在传播1英里的距离需要约5秒钟。你可以通过计算闪电闪光和雷声之间的时间来估计雷暴的距离;如果你数到5秒钟,那么暴雨距离约为1英里。可听范围内的声音速度受温度的显著影响,稍微受湿度的影响。它不受声音强度、频率或大气压力的显著影响。在某些情况下,原本会影响声音速度的某些因素被其他因素抵消,从而产生微不足道的变化。
声音在介质中传播的速度取决于该介质本身和其他因素。其他条件相同,介质越坚硬或刚性越大,或者可压缩性越小,声音在其中传播的速度就越快。一般来说,声音在液体中的传播速度比在空气中快,而在固体中的传播速度又比在液体中快。例如,声音在海水中的传播速度约为5,023英尺/秒,在钢中的传播速度约为16,570英尺/秒。其他示例见表1-1。正如前面提到的,随着温度的升高,声音在空气中的传播速度也会增加(每华氏度约增加1.1英尺/秒)。最后,湿度对空气中的声音速度有轻微影响;空气越湿,速度越快。需要注意的是,声音的速度与粒子速度不同。声音的速度确定了声能在媒质中传播的快慢。粒子速度由声音的响度决定。
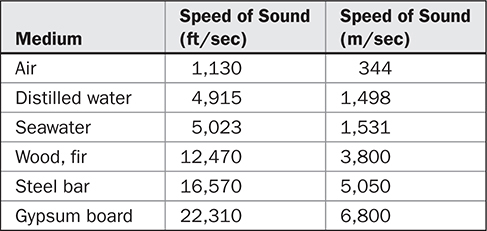
TABLE 1-1 不同材料中声音速度的示例
波长和频率
正弦波在图1-7中进行了说明。波长 λ 是波在完成一个周期所需的时间内所传播的距离。可以通过连续的峰值之间或周期上的任意两个对应点之间来测量波长。这对于除正弦波以外的周期性波也适用。频率 f 表示每秒的周期数,以赫兹(Hz)为单位。频率和波长的关系如下所示:
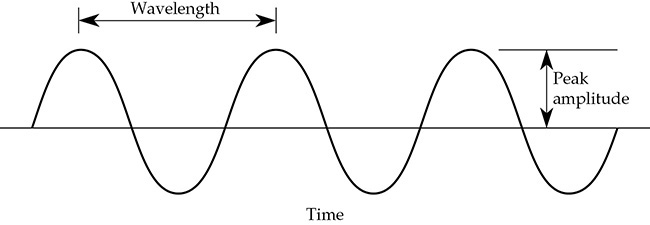
FIGURE 1-7 波长是波在完成一个周期所需的时间内所传播的距离。它也可以表示为周期性波上的一个点到下一个周期波上相应点的距离。
也可以写成:
如前所述,空气中声音的速度在常规条件下约为1,130英尺/秒。对于在空气中传播的声音,式(1-2)变为:
这个关系可能是音频领域中最基本重要的关系之一。在图1-8中,给出了两种用图形解决式(1-3)的方法。
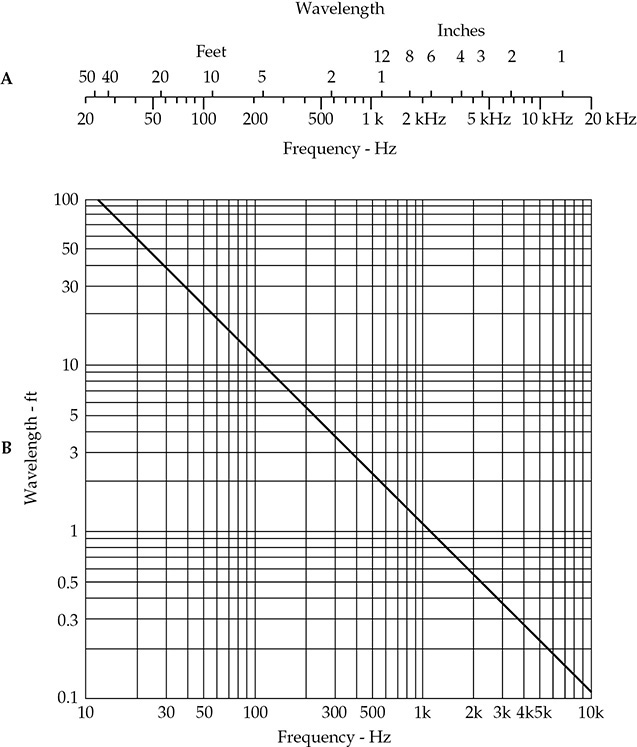
FIGURE 1-8 波长和频率呈反比关系。 (A)频率——波长近似换算刻度。 (B)用于确定不同频率声波在空气中的波长的图表。 (两者都基于声速1,130英尺/秒。)
复杂波形
语音和音乐的波形与简单的正弦波有着显著的差异,被视为复杂波形。然而,无论波形多么复杂,只要它是周期性的,就可以将其分解为正弦分量。反过来,任何复杂的周期性波形都可以由具有不同频率、不同振幅和不同时间关系(相位)的正弦波合成。约瑟夫·傅里叶是第一个证明了这些关系的人³译注:1822 The Analytical Theory of Heat 。这个概念很简单,但在具体的语音或音乐声音中应用时往往很复杂。让我们看看如何将复杂周期性波形简化为简单的正弦波分量。
谐波
在图1-9A中,显示了一个给定幅度和频率 f1 的简单正弦波。 图1-9B显示了第二谐波正弦波 f2,它的频率是 f1 的两倍,振幅为 f1 的一半。将 f1 和 f2 在每个时间点上组合起来,得到了图1-9C的波形。 图1-9D显示了第三谐波正弦波 f3,它的频率是 f1 的三倍,振幅为 f1 的一半。将其添加到 C 的 f1 + f2 波形中,得到了图1-9E。简单的正弦波 图1-9A 在添加了其他正弦波之后逐渐变化;这对声学波和电子信号都是有效的。这个过程可以反过来。可以通过声学或电子滤波器将图1-9E的复杂波形解构为简单的 f1、f2 和 f3 正弦分量。例如,将图1-9E的波形通过只允许 f1 并拒绝 f2 和 f3 的滤波器,原始的 f1 正弦波 图1-9A 将以原始的状态出现。
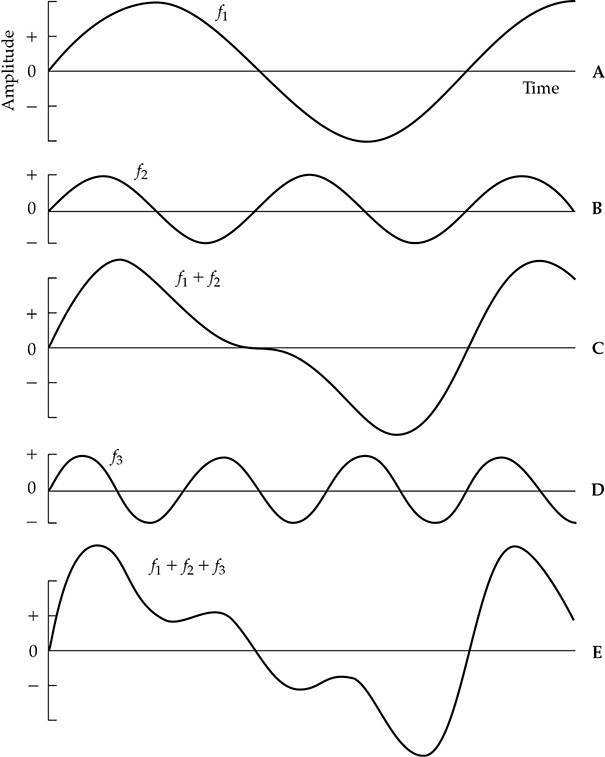
图1-9 正弦波组合的研究。 (A) 基频 f1。 (B) 第二谐波 f2,它的频率是 f1 的两倍,振幅为 f1 的一半。 (C) 通过逐点相加得到的 f1 和 f2 的和。 (D) 第三谐波 f3,它的频率是 f1 的三倍,振幅为 f1 的一半。 (E) 由 f1、f2 和 f3 相加得到的波形。所有三个分量处于相位一致的状态;也就是说,它们都在同一时间从零开始。
在图1-9A中,具有最低频率 (f1) 的正弦波被称为基频,具有两倍频率 (f2) 的正弦波在图1-9B中被称为第二谐波,而具有三倍频率 (f3) 的正弦波在图1-9D中被称为第三谐波。第四谐波和第五谐波分别是基频的四倍和五倍频率,依此类推。
相位
在图1-9中,所有三个分量,f1、f2 和 f3,同时开始。这被称为相位一致的条件。在许多情况下,谐波之间以及谐波与基频之间的时间关系与此相当不同。我们观察到,汽车发动机的曲轴旋转一周 (360°) 相当于活塞的简谐运动的一个周期。活塞的上下运
动在时间上形成了图1-10中的正弦波。一个完整的正弦波周期代表了 360° 的旋转。如果另一个具有相同频率的正弦波延迟了 90°,它与第一个正弦波的时间关系是一个四分之一波长的延迟 (时间向右增加)。半波延迟将是 180°,依此类推。对于 360° 的延迟,图1-10底部的波形与顶部波形同步,同时达到正峰值和负峰值,并再次产生相位一致的条件。
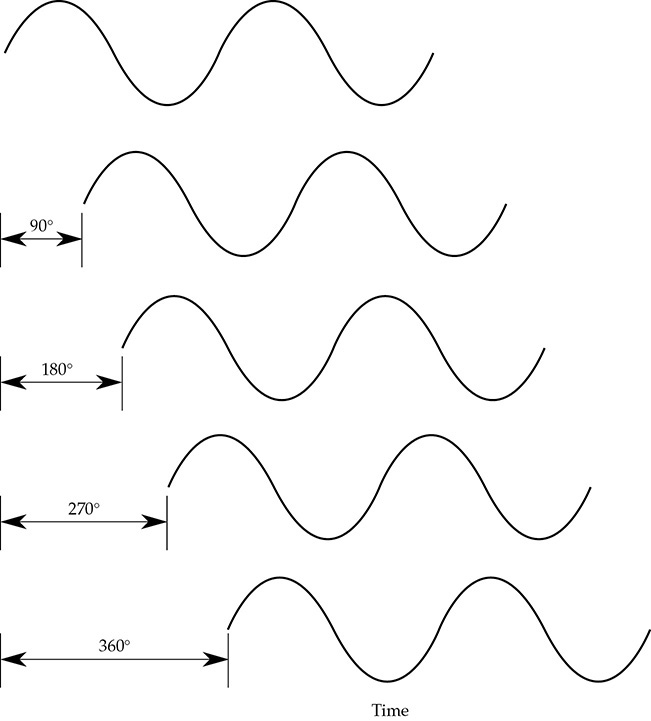
图1-10 同一振幅和频率的波形之间的相位关系示例。360° 的旋转类似于一个完整的正弦波周期。
再次参考图1-9,图1-9E中的复合波形的所有三个分量处于相位一致的状态。也就是说,基频 f1、第二谐波 f2 和第三谐波 f3 都在同一时间从零开始。如果谐波与基频不同相位会发生什么?图1-11说明了这种情况。第二谐波 f2 现在比 f1 提前90°,而第三谐波 f3 比 f1 滞后90°。通过在每个时刻结合 f1、f2 和 f3,并注意正负号,可以得到图1-11E中的扭曲波形。

图1-11 正弦波组合的相位不一致研究。 (A) 基频 f1。 (B) 第二谐波 f2,它的频率是 f1 的两倍,振幅为 f1 的一半,相位提前 f1 的 90°。 (C) 通过逐点相加得到的 f1 和 f2 的组合。 (D) 第三谐波 f3,它的频率是 f1 的三倍,振幅为 f1 的一半,相位滞后 f1 的 90°。 (E) f1、f2 和 f3 的总和。将这个结果与图1-9E中的波形进行比较。波形的差异完全是由于谐波相对于基频的相位偏移所致。
在图1-9E和图1-11E之间的差异在于在谐波f2和f3之间以及基频f1之间引入了相位偏移。这就是产生结果波形剧烈变化所需的全部条件。奇怪的是,尽管通过改变分量之间的时间关系可以显著改变波形的形状,但耳朵对于这种变化相对不敏感。换句话说,虽然图1-9和图1-11中的波形E在视觉上非常不同,但听起来它们听起来非常相似。
一个常见的错误是将极性与相位混淆。相位是两个信号之间的时间关系,而极性是给定一对信号引线之间的+/—或—/ +关系。
谐振
音乐家可能倾向于使用"partials"而不是"harmonic"这个术语,但最好在这两个术语之间做出区分,因为某些乐器的谐振与基频不成谐振关系。也就是说,谐振可能不是基频频率的精确倍数,但通过这种与真正的谐振关系偏离的方式仍然可以赋予音色丰富性。例如,打击乐器(如钟、铙钹和风铃)的谐振与基频不成谐振关系。
八度
音频工程师和声学家经常使用谐波的整数倍概念,因为它与声音的物理特性密切相关。音乐家经常提到八度,这是一个对数概念,在音乐音阶和术语中具有牢固的地位,因为它与耳朵的特性有关。音频人员也与人耳有关;因此,他们常常使用频率的对数刻度、对数测量单位和基于八度的各种设备。
在图1-12中比较了谐波和八度。谐波是线性相关的;每一个下一个谐波是前一个的整数倍。八度被定义为两个频率的2:1比例。例如,中音C(C4)的频率接近261 Hz。稍高一音的C(C5)的频率约为522 Hz。频率之间的比率是音乐音阶的一部分。频率比例2:1是八度;比例3:2是五度;比例4:3是四度,依此类推。
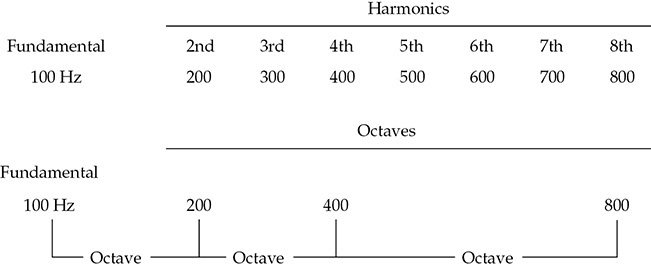
FIGURE 1-12 谐波和八度的比较。谐波是线性相关的;八度是对数相关的。
从100 Hz到200 Hz的间隔是一个八度,从200 Hz到400 Hz的间隔也是一个八度。从100 Hz到200 Hz的间隔被感知为比从200 Hz到300 Hz的间隔更大;这说明耳朵感知间隔时是以比例而不是算术差异为基础的。特别是,我们对频率的感知是对数的。由于八度在声学工作中很重要,因此考虑一下八度的数学(内涵)是很有用的。
八度的定义是2:1的比例关系,它的数学表达式为:
其中,f2 = 八度间隔上限的频率,单位为Hz
f1 = 八度间隔下限的频率,单位为Hz
n = 八度的数量
对于一个八度,n = 1,方程(1-4)变为 f2/f1 = 2,这就是八度的定义。方程(1-4)的其他应用如下:
例1 如果一个频带的低频限制是20 Hz,那么宽度为10个八度的频带的高频限制是多少?
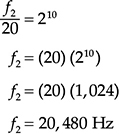
例2 如果446 Hz是1/3八度带的下限,那么上限的频率是多少?
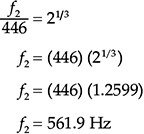
例3 一个以1,000 Hz为中心的1/3八度带的下限是多少? f1 是1,000 Hz,但是下限将比1/3八度带低1/6八度,因此 n = 1/6:

例4 以2,500 Hz为中心的一个八度带的下限频率是多少?
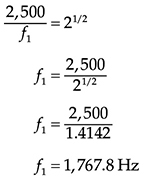
上限阈值是多少?
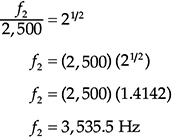
在许多声学应用中,声音被分为八个八度带,其中心频率为63、125、250、500、1,000、2,000、4,000和8,000 Hz。在某些情况下,声音被分为1/3八度带,其中心频率为31.5、50、63、80、100、125、160、200、250、315、400、500、630、800、1,000、1,250、1,600、2,000、2,500、3,150、4,000、5,000、6,300、8,000和10,000 Hz。
频谱
被普遍接受的可听频谱范围是20 Hz至20 kHz。这是落在人耳感知限度内的频率范围,也是人耳的特定特征之一。在这里,通过正弦波和谐波的上下文,我们可以建立频谱的概念。可见光谱在听觉上的对应物是可听频谱。我们无法看到远紫外线光,因为其电磁能量的频率对于眼睛来说太高而无法感知。我们也无法看到远红外线光,因为其频率太低。同样,有些声音的频率对于耳朵来说太低(次声音)或太高(超声音)而无法听到。
图1-13展示了几个代表音频中无限数量不同波形的波形图。这些波形是由信号发生器产生并在示波器上捕获的。在每个捕获图像的右侧是该特定信号的频谱。频谱显示了信号能量在频率上的分布情况。除了图1-13D的信号外,频谱的可听范围经过了具有5 Hz带宽的非常锐利的滤波器的处理。通过这种方式,能量的浓度被定位和测量。
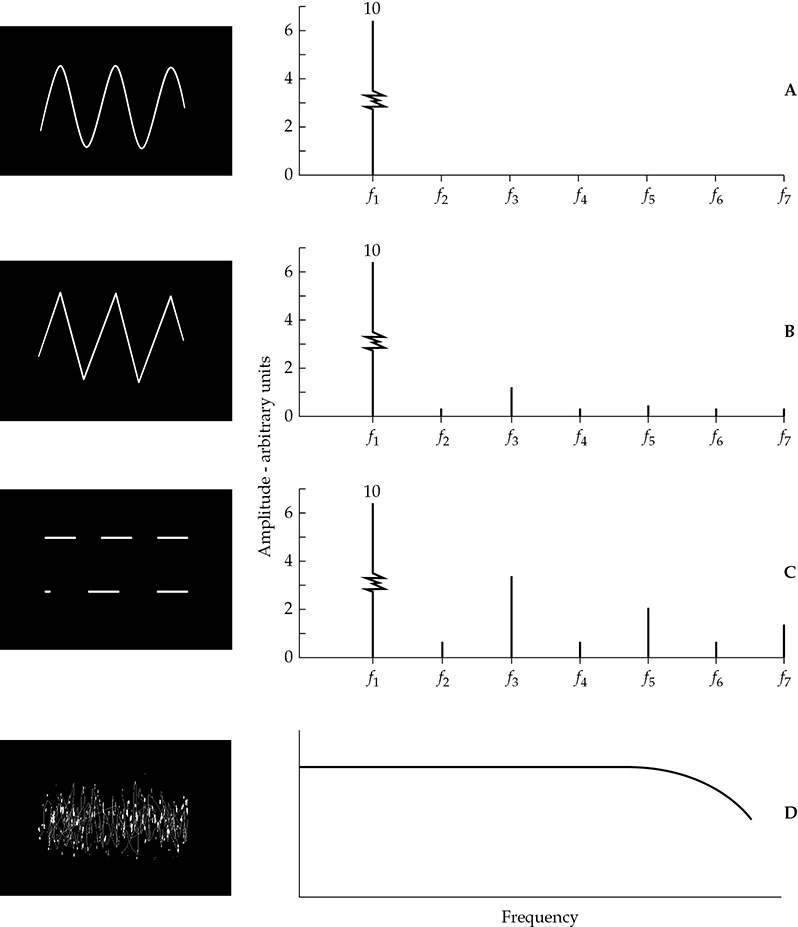
图1-13基本波形和噪声的比较。(A)纯正弦波的频谱能量完全集中在一个频率上。(B)三角波和(C)方波的波形各自具有一个突出的基波和许多倍频的谐波。(D)白噪声的能量在频谱上均匀分布,直到某一点开始衰减。随机噪声可以被视为具有连续频谱的统计分布信号。
对于正弦波,所有的能量集中在一个基频上,没有谐波。正如我们所见,这是正弦波的定义特性。在图1-13A中,由这个特定信号发生器产生的正弦波并不是纯正弦波。存在一些无关的谐波成分,这是对正弦波的畸变,但在扫描其频谱时,检测到的谐波幅度过低,不足以在图上显示。
在图1-13B中显示的三角波形具有一个主要的基波分量,幅度为10单位。波形分析仪检测到一个显著的二次谐波分量,在基波频率的两倍频率f2上,幅度为0.21单位。第三次谐波的幅度为1.13单位,第四次谐波的幅度为0.13单位,依此类推。第七次谐波的幅度为0.19单位,第十四次谐波(在本例中约为15 kHz)的幅度仅为0.03单位。我们可以看到,这个三角波形在可听频谱范围内具有适度振幅的奇次和偶次成分。如果我们知道每个成分的幅度和相位,就可以通过组合它们来合成原始的三角波形。
通过类似的分析,我们可以得到图1-13C所示方波的频谱。方波的谐波幅度比三角波大得多,明显更偏向于奇次谐波而不是偶次谐波。第三次谐波的幅度为基波的34%。方波的第十五次谐波(未显示)为0.52单位。图1-14A显示了一个方波,可以通过向基波添加谐波来合成。然而,需要很多谐波。例如,图1-14B显示了添加两个非零谐波分量所得到的波形,图1-14C显示了添加九个非零谐波分量所得到的结果。这说明为什么带限制的“方波”没有方形的外观。
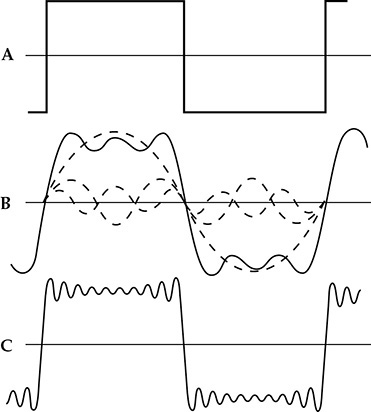
图1-14方波可以通过向正弦波基频添加谐波来合成。(A)一个方波(具有无限多个谐波分量)。 (B)基波和两个非零谐波分量的总和。 (C)基波和九个非零谐波分量的总和。显然,需要很多分量来平滑波纹并产生(A)的方形边缘。
正弦波、三角波和方波的频谱显示能量集中在谐波频率上,但在频谱中间没有能量分布。这些都是周期性的波形,它们在周期之后重复出现。在图1-13D中的第四个示例是一个随机噪声信号,特别是均匀分布在不同频率上的白噪声信号。由于波动性太大,无法获得准确的读数,因此无法通过具有5 Hz通带的波形分析仪对该信号进行满意的测量。通过采用固定带宽的较宽通带以及使用各种积分设备来获得稳定指示,可以获得所示的频谱形状。该频谱告诉我们,随机噪声信号的能量在整个频谱范围内均匀分布;高频处的衰减表示随机噪声发生器的上限频率已经达到。该信号仍被视为白噪声,因为其能量谱在感兴趣的带宽范围内是平坦的。
在示波器上显示的正弦波和随机噪声信号之间几乎没有视觉相似性,然而它们之间存在隐藏的关系。即使随机噪声也可以被视为由频率、幅度和相位不断变化的正弦波分量组成。如果我们将随机噪声通过一个窄带滤波器并在示波器上观察滤波器的输出,我们将看到一个不断变化幅度的不安定的类似正弦波的波形。理论上,一个无限窄的滤波器将筛选出一个纯正弦波。
要点
• 声音存在于气体、固体和液体等弹性介质中的波动。
• 简谐运动是一种基本的振荡运动,产生正弦波。
• 声音的传播是由于动量从一个粒子传递到另一个粒子。
• 空气中声音的速度大约为1130英尺/秒,根据介质的特性和其他因素而变化。
• 声音的波长是波在完成一个周期所需的时间内传播的距离。
• 语音和音乐的波形是复杂的波形。如果它们是周期性的,可以将它们简化为称为谐波的正弦分量。
• 相位描述了波形之间的时间关系。
• 可听频谱的常用接受范围是20 Hz到20 kHz;这是人耳感知范围内的频率近似范围。